题目内容
14.设向$\overrightarrow{a}$=(x-1,2)$\overrightarrow{b}$=(4,x+1),则“x=-3”是$\overrightarrow{a}$∥$\overrightarrow{b}$”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 由向量共线的坐标表示求出x的值为±3,从而可知“x=-3”是$\overrightarrow{a}$∥$\overrightarrow{b}$”的充分不必要条件.
解答 解:∵$\overrightarrow{a}$=(x-1,2)$\overrightarrow{b}$=(4,x+1),
∴由$\overrightarrow{a}$∥$\overrightarrow{b}$,得(x-1)(x+1)-8=0,解得:x=±3.
∴“x=-3”是$\overrightarrow{a}$∥$\overrightarrow{b}$”的充分不必要条件.
故选:A.
点评 平行问题是一个重要的知识点,在高考题中常常出现,常与向量的模、向量的坐标表示等联系在一起,要特别注意垂直与平行的区别.若$\overrightarrow{a}$=(a1,a2),$\overrightarrow{b}$=(b1,b2),则$\overrightarrow{a}$⊥$\overrightarrow{b}$?a1a2+b1b2=0,$\overrightarrow{a}$∥$\overrightarrow{b}$?a1b2-a2b1=0,是基础题.

练习册系列答案
相关题目
6.已知f(x)=10x,g(x)=2x,x0<0,则( )
| A. | 1>f(x0)>g(x0) | B. | 1>g(x0)>f(x0) | C. | f(x0)>g(x0)>1 | D. | g(x0)>f(x0)>2 |
4.函数y=3${\;}^{ax-{x}^{2}}$在区间(1,+∞)上单调递减,则实数a的取值范围是( )
| A. | (-∞,2) | B. | (2,+∞) | C. | (-∞,2] | D. | [2,+∞) |
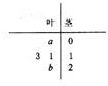 如图所示是某组数据的茎叶图,已知该组数据的平均数为$\frac{23}{2}$,ab=1(a,b∈R),则$\frac{a}{2}sin2x+bco{s}^{2}x-\frac{b}{2}$的最大值为$\frac{\sqrt{2}}{2}$.
如图所示是某组数据的茎叶图,已知该组数据的平均数为$\frac{23}{2}$,ab=1(a,b∈R),则$\frac{a}{2}sin2x+bco{s}^{2}x-\frac{b}{2}$的最大值为$\frac{\sqrt{2}}{2}$.