题目内容
19.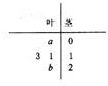 如图所示是某组数据的茎叶图,已知该组数据的平均数为$\frac{23}{2}$,ab=1(a,b∈R),则$\frac{a}{2}sin2x+bco{s}^{2}x-\frac{b}{2}$的最大值为$\frac{\sqrt{2}}{2}$.
如图所示是某组数据的茎叶图,已知该组数据的平均数为$\frac{23}{2}$,ab=1(a,b∈R),则$\frac{a}{2}sin2x+bco{s}^{2}x-\frac{b}{2}$的最大值为$\frac{\sqrt{2}}{2}$.
分析 根据题意先求出a、b的值,再化简$\frac{a}{2}sin2x+bco{s}^{2}x-\frac{b}{2}$,求出它的最大值.
解答 解:∵ab=1①,$\frac{a+11+13+(20+b)}{4}$=$\frac{23}{2}$②,
∴由①②解得a=b=1;
∴$\frac{a}{2}sin2x+bco{s}^{2}x-\frac{b}{2}$=$\frac{1}{2}$sin2x+cos2x-$\frac{1}{2}$
=$\frac{1}{2}$sin2x+$\frac{1}{2}$cos2x
=$\frac{\sqrt{2}}{2}$($\frac{\sqrt{2}}{2}$sin2x+$\frac{\sqrt{2}}{2}$cos2x)
=$\frac{\sqrt{2}}{2}$sin(2x+$\frac{π}{4}$)≤$\frac{\sqrt{2}}{2}$,
∴该式的最大值是$\frac{\sqrt{2}}{2}$.
故答案为:$\frac{\sqrt{2}}{2}$.
点评 本题考查了茎叶图的应用问题,也考查了三角函数的恒等变换与应用问题,是基础题目.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
10.设向量$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),$\overrightarrow{c}$=(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),x$\overrightarrow{a}$+y$\overrightarrow{b}$+z$\overrightarrow{c}$=(1,0)(x,y,z∈R),则x2+y2+z2的最小值为( )
| A. | $\frac{2}{3}$ | B. | 1 | C. | $\frac{4}{3}$ | D. | 2 |
14.设向$\overrightarrow{a}$=(x-1,2)$\overrightarrow{b}$=(4,x+1),则“x=-3”是$\overrightarrow{a}$∥$\overrightarrow{b}$”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |