题目内容
【题目】已知函数f(x)=ex﹣![]() 有两个极值点.
有两个极值点.
(1)求实数a的取值范围;
(2)若函数f(x)的两个极值点分别为x1,x2,求证:x1+x2>2.
【答案】(1)(e,+∞);(2)见解析
【解析】
(1)f′(x)=ex﹣ax.函数f(x)=ex![]() 有两个极值点f′(x)=ex﹣ax=0有两个实数根.x=0时不满足上述方程,方程化为:a
有两个极值点f′(x)=ex﹣ax=0有两个实数根.x=0时不满足上述方程,方程化为:a![]() ,令g(x)
,令g(x)![]() ,(x≠0).利用导数已经其单调性即可得出.
,(x≠0).利用导数已经其单调性即可得出.
(2)由(1)可知:a>e时,函数f(x)有两个极值点分别为![]() ,x2,不妨设
,x2,不妨设![]() <
<![]() ,
,![]() +
+![]() >2
>2![]() >2﹣
>2﹣![]() >1
>1![]() ,由
,由![]() ,因此即证明:
,因此即证明:![]() .构造函数h(x)
.构造函数h(x)![]() ,0<x<1,2﹣x>1.利用导数已经其单调性即可得出.
,0<x<1,2﹣x>1.利用导数已经其单调性即可得出.
(1)解:f′(x)=ex﹣ax.
∵函数f(x)=ex![]() 有两个极值点.
有两个极值点.
∴f′(x)=ex﹣ax=0有两个实数根.
x=0时不满足上述方程,
方程化为:a![]() ,
,
令g(x)![]() ,(x≠0).
,(x≠0).
g′(x)![]() ,
,
可得:x<0时,g′(x)<0,函数g(x)单调递减;0<x<1时,g′(x)<0,函数g(x)单调递减;x>1时,g′(x)>0,函数g(x)单调递增.
g(1)=e,得到函数草图如图所示.
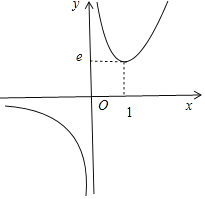
a>e时,方程f′(x)=ex﹣ax=0有两个实数根.
∴实数a的取值范围是(e,+∞).
(2)证明:由(1)可知:a>e时,函数f(x)有两个极值点分别为x1,x2,不妨设x1<x2.
证明:![]() +
+![]() >2
>2![]() >2﹣
>2﹣![]() >1
>1![]() ,
,
由![]() ,因此即证明:
,因此即证明:![]() .
.
构造函数h(x)![]() ,0<x<1,2﹣x>1.
,0<x<1,2﹣x>1.
h′(x)![]() (x﹣1)
(x﹣1)![]() ,
,
令函数u(x)![]() ,(0<x<2).
,(0<x<2).
u′(x)![]() .
.
可得函数u(x)在(0,2)内单调递减,于是函数v(x)![]() 在(0,1)内单调递减.
在(0,1)内单调递减.
v(x)≥v(1)=0.∴h′(x)![]() (x﹣1)
(x﹣1)![]() ,h(x)在(0,1)内单调递减.
,h(x)在(0,1)内单调递减.
∴h(x)>h(1)=0,
∴![]() .
.
因此![]() +
+![]() >2成立.
>2成立.

 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案