��Ŀ����
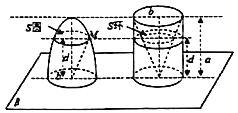
����Ŀ���ҹ�����ʱ������ѧ���敜�����һ��ԭ���������Ƽ�ͬ����������족.��˼�ǣ������ȸߵļ������������еȸߴ���ˮƽ����������ȣ����������������������.����������Բ��������ת���ɵ���ת��.��ͼ��������ֱ����Ϊ![]() ���߽�Ϊ
���߽�Ϊ![]() ���ְ�������ѱ���ȥ��Բ���Բ��������ͬһƽ��
���ְ�������ѱ���ȥ��Բ���Բ��������ͬһƽ��![]() �ϣ���ƽ����ƽ��
�ϣ���ƽ����ƽ��![]() ����ƽ��
����ƽ��![]() �������
�������![]() ����ƽ��������������壬�ɺ�صõ�
����ƽ��������������壬�ɺ�صõ�![]() ��
��![]() ������.����֤��
������.����֤��![]() �ܳ���.�ݴˣ�����᳤Ϊ1���볤�᳤Ϊ3��������������_______��
�ܳ���.�ݴˣ�����᳤Ϊ1���볤�᳤Ϊ3��������������_______��
���𰸡�![]()
��������
��ѧ���敜ԭ���������Ƽ�ͬ����������족��������һԭ�������Եõ�������������Ϊ![]() ���Ӷ��õ�������������������⡣
���Ӷ��õ�������������������⡣
�⣺��Ϊ![]() �ܳ���
�ܳ���
�������������Ϊ![]()
���ԣ�����������Ϊ![]() ��
��
��Ϊ������İ���᳤Ϊ1���볤�᳤Ϊ3
���ԣ�����������Ϊ![]() ��
��
�ʴ���![]() ��
��

����Ŀ��Ϊ�˵���һ����ӻ���ʹ��ʱ�䣬�о���Ա�Ըÿ���ӻ���������Ӧ�IJ��ԣ����õ�������ͳ������ͼ��ʾ��

���Բ�ͬ����������������ӻ��Ĺ�����Ը�������飬�õ����������±���ʾ��
Ը��������ӻ� | ��Ը��������ӻ� | �ܼ� | |
40������ | 800 | 1000 | |
40������ | 600 | ||
�ܼ� | 1200 |
��1������ͼ�е����ݣ��Թ��Ƹÿ���ӻ���ƽ��ʹ��ʱ�䣻
��2�����ݱ������ݣ��ж��Ƿ���99.9%�İ�����Ϊ��Ը���ÿ���ӻ����롰��������䡱�йأ�
��3�������յ��ӻ���ʹ��ʱ����зֲ��������ʹ��ʱ����![]() ��
��![]() �ĵ��ӻ��г�ȡ5̨���ٴ���5̨�������ȡ2̨���������⣬��ȡ��2̨���ӻ���ʹ��ʱ�䶼��
�ĵ��ӻ��г�ȡ5̨���ٴ���5̨�������ȡ2̨���������⣬��ȡ��2̨���ӻ���ʹ��ʱ�䶼��![]() �ڵĸ��ʣ�
�ڵĸ��ʣ�
���� | 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
����Ŀ��ij�г��о���ԱΪ���˽��ҵ�����ļ�˾ǰ�ڵľ�Ӫ״�����Ըù�˾2018�����������µ����������ͳ�ƣ������ݵõ������ݻ�������Ӧ������ͼ����ͼ��ʾ
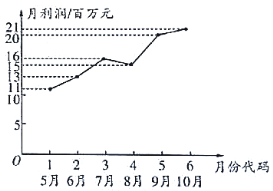
��1��������ͼ���Կ������������Իع�ģ�����������![]() ����λ������Ԫ�����·ݴ���
����λ������Ԫ�����·ݴ���![]() ֮��Ĺ�ϵ����
֮��Ĺ�ϵ����![]() ����
����![]() �����Իع鷽�̣���Ԥ��ù�˾2019��3�·ݵ�����
�����Իع鷽�̣���Ԥ��ù�˾2019��3�·ݵ�����
��2����˾��������һ���Ʒ����Ҫ�ɹ�һ�����Ͳ��ϣ�����![]() ��
��![]() �����ͺŵ����Ͳ��Ͽɹ�ѡ���涨ÿ�����Ͳ�������ʹ��
�����ͺŵ����Ͳ��Ͽɹ�ѡ���涨ÿ�����Ͳ�������ʹ��![]() ���£����²��ϵIJ��ȶ��Իᵼ�²�����������ͬ���ֶ�
���£����²��ϵIJ��ȶ��Իᵼ�²�����������ͬ���ֶ�![]() ��
��![]() �����ͺŵ����Ͳ��϶�Ӧ�IJ�Ʒ��
�����ͺŵ����Ͳ��϶�Ӧ�IJ�Ʒ��![]() �����п�ѧģ����ԣ��õ��������Ͳ���ʹ��������Ƶ��ͳ�����±���
�����п�ѧģ����ԣ��õ��������Ͳ���ʹ��������Ƶ��ͳ�����±���
ʹ������ �������� |
|
|
|
| �ܼ� |
|
|
|
|
|
|
|
|
|
|
|
|
������Ǽ�˾�ĸ����ˣ����ѡ��ɹ��Ŀ����Ͳ��ϣ�
�ο����ݣ�![]() ��
��![]() .�ο���ʽ���ع�ֱ�߷���Ϊ
.�ο���ʽ���ع�ֱ�߷���Ϊ![]() ������
������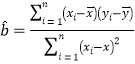
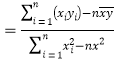 .
.
