题目内容
【题目】已知函数![]() .
.
(1)求不等式![]() 的解集;
的解集;
(2)如果![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
【答案】(1) (∞, ![]() ]∪[
]∪[![]() ,+∞);(2)
,+∞);(2)![]() .
.
【解析】试题分析:(1)零点分区间,去绝对值,分段解不等式(2)恒成立求参,变量分离,转化为求函数最值.
(1)当x<3时,f(x)=3x+(4x)=72x
不等式f(x)2即72x2,解之得x52;
当3x4时,f(x)=x3+(4x)=1,不等式f(x)2的解集为空集;
当x>4时,f(x)=x3+(x4)=2x7,
不等式f(x)2即2x72,解之得x92
综上所述,原不等式的解集为(∞, ![]() ]∪[
]∪[![]() ,+∞);
,+∞);
(2)f(x) ![]() a恒成立,即f(x)的最小值
a恒成立,即f(x)的最小值![]() a,
a,
由(1)可得f(x)在(∞,3)上是减函数,在[3.4]上是常数1,
在区间(4,+∞)上是增函数。
∴函数f(x)的最小值为1,
由此可得a![]() 1,即实数a的取值范围为
1,即实数a的取值范围为![]() .
.

【题目】汽车厂生产![]() 三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
轿车 | 轿车 | 轿车 | |
舒适型 | 100 | 150 |
|
标准型 | 300 | 450 | 600 |
(1)求![]() 的值;
的值;
(2)用分层抽样的方法在![]() 类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取
类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取
2辆,求至少有1辆舒适型轿车的概率;
(3)用随机抽样的方法从![]() 类舒适型轿车中抽取8辆,经检测它们的得分如下:
类舒适型轿车中抽取8辆,经检测它们的得分如下:![]() . 把这8辆轿车的得分看成一个总体,从中任取一个数,求该数与样本平均数之差的绝对 值不超过
. 把这8辆轿车的得分看成一个总体,从中任取一个数,求该数与样本平均数之差的绝对 值不超过![]() 的概率.
的概率.
【题目】某地区2010年至2016年农村居民家庭纯收入![]() (单位:千元)的数据如下表
(单位:千元)的数据如下表
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求![]() 关于
关于![]() 的线性回归方程。
的线性回归方程。
(2)判断![]() 与
与![]() 之间是正相关还是负相关?
之间是正相关还是负相关?
(3)预测该地区2018年农村居民家庭人均纯收入。
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
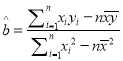 ,
, ![]()
