题目内容
7.函数y=Asin(ωx+φ)+B的部分图象如下图所示,设A>0,ω>0,|φ|<$\frac{π}{2}$,则$f(\frac{π}{3})$=3.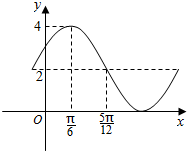
分析 求出函数的周期,求出ω,利用图象求出A,b,然后通过函数图象经过的特殊点求出φ即可求$f(\frac{π}{3})$的值.
解答 解:由函数的图象可知:A=2,B=2,T=4×($\frac{5π}{12}$-$\frac{π}{6}$)=π,所以ω=2,
因为函数的图象经过($\frac{π}{6}$,4),
所以4=2sin(2×$\frac{π}{6}$+φ)+2,即1=sin($\frac{π}{3}$+φ),因为|φ|<$\frac{π}{2}$,所以φ=$\frac{π}{6}$,
所以:f($\frac{π}{3}$)=2sin(2×$\frac{π}{3}$+$\frac{π}{6}$)+2=3,
故答案为:3.
点评 本题考查三角函数的解析式的求法,注意函数的图象的应用,考查分析问题解决问题的能力,属于中档题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
15.已知tanα=2,则sin2α的值为( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
16.在正三棱锥P-ABC中,M为△ABC内(含边界)一动点,且点M到三个侧面PAB、PBC、PCA的距离成等差数列,则点M的轨迹是( )
| A. | 一条折线段 | B. | 一条线段 | C. | 一段圆弧 | D. | 一段抛物线 |
17.如图所示的程序运行结果为( )
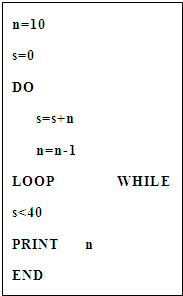
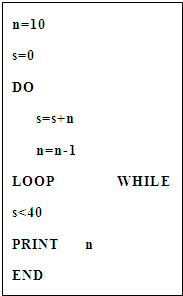
| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
 如图,已知三棱柱ABC---A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M,N分别为CC1,BC的中点,点P为直线A1B1上一点,且满足$\overrightarrow{{A_1}P}=λ\overrightarrow{{A_1}{B_1}}$,
如图,已知三棱柱ABC---A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M,N分别为CC1,BC的中点,点P为直线A1B1上一点,且满足$\overrightarrow{{A_1}P}=λ\overrightarrow{{A_1}{B_1}}$, 一个体积为16$\sqrt{3}$的正三棱柱(即底面为正三角形,侧棱垂直底面)的三视图如图所示,则这个三棱柱的左视图的面积为8$\sqrt{3}$.
一个体积为16$\sqrt{3}$的正三棱柱(即底面为正三角形,侧棱垂直底面)的三视图如图所示,则这个三棱柱的左视图的面积为8$\sqrt{3}$.