题目内容
19.已知f(x)=ax-lnx,x∈(0,e],其中e是自然对数的底数,a∈R.(1)当a=1时,求函数f(x)的极值;
(2)是否存在实数a使函数f(x)的最小值是3?若存在,求出a的值;若不存在,说明理由;
(3)在(1)的条件下,证明不等式f(x)>$\frac{lnx}{x}$+$\frac{1}{2}$,x∈(0,e]恒成立.
分析 (1)将a=1代入函数的表达式,求出f(x)的导数,得到函数f(x)的单调区间,从而求出函数的极值;
(2)先求出函数f(x)的导数,通过讨论a的范围,得到函数的单调区间,从而求出a的值;
(3)令g(x)=$\frac{lnx}{x}$+$\frac{1}{2}$,x∈(0,e],通过求出g(x)的导数,得到g(x)的单调区间,从而求出故g(x)max,进而得到f(x)min>g(x)max,问题得证.
解答 解:(1)当a=1时,f(x)=x-lnx,f′(x)=1-$\frac{1}{x}$=$\frac{x-1}{x}$,x∈(0,e],
令f′(x)>0,解得:1<x≤e,令f′(x)<0,解得:0<x<1,
∴函数f(x)在(0,1)上单调递减,在(1,e]上单调递增,
且当x∈(0,e]时,f(x)有极小值f(1)=1;
(2)由f(x)=ax-lnx,得f′(x)=a-$\frac{1}{x}$=$\frac{ax-1}{x}$,x∈(0,e],
当a≤$\frac{1}{e}$时,有f′(x)≤0恒成立,此时函数在(0,e]上单调递减,
∴f(x)min=f(e)=ae-lne=ae-1=3,∴a=$\frac{4}{e}$(舍),
当a>$\frac{1}{e}$时,令f′(x)>0,解得:$\frac{1}{a}$<x<e,令f′(x)<0,解得:0<x<$\frac{1}{a}$,
∴函数f(x)在(0,$\frac{1}{a}$)单调递减,在($\frac{1}{a}$,e)上单调递增,
∴f(x)min=f($\frac{1}{a}$)=1-ln$\frac{1}{a}$=3,∴a=e2,
综上,a=e2时满足条件.
(3)由(1)知,当x∈(0,e)时,f(x)有极小值f(1)=1,
令g(x)=$\frac{lnx}{x}$+$\frac{1}{2}$,x∈(0,e],则g′(x)=$\frac{1-lnx}{{x}^{2}}$,
当x∈(0,e]时,g(x)>0,则g(x)在(0,e]上单调递增,
故g(x)max=g(e)=$\frac{1}{e}$+$\frac{1}{2}$,
∴f(x)min>g(x)max,
因此,不等式f(x)>$\frac{lnx}{x}$+$\frac{1}{2}$,x∈(0,e]恒成立.
点评 本题考察了函数的单调性,极值问题,考察导数的应用,是一道中档题.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案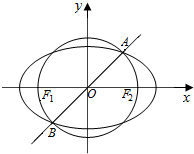 知点F1(-1,0)和点F2(1,0),以F1、F2为焦点的椭圆和以线段F1F2为直径的圆于第一、三象限交于A,B两点,直线AB的斜率为k,若0<k≤$\sqrt{3}$,则此椭圆的离心率e的取值范围为[$\sqrt{3}$-1,1).
知点F1(-1,0)和点F2(1,0),以F1、F2为焦点的椭圆和以线段F1F2为直径的圆于第一、三象限交于A,B两点,直线AB的斜率为k,若0<k≤$\sqrt{3}$,则此椭圆的离心率e的取值范围为[$\sqrt{3}$-1,1).