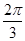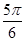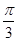题目内容
设函数f(x)=
•
,其中向量
=(2cosx,1),
=(cosx,
sin2x)(x∈R)
(1)求f(x)的最小正周期;
(2)在△ABC中,a,b,c分别是角A,B,C的对边,f(A)=2,a=
,b+c=3,b>c,求b,c的长.
| a |
| b |
| a |
| b |
| 3 |
(1)求f(x)的最小正周期;
(2)在△ABC中,a,b,c分别是角A,B,C的对边,f(A)=2,a=
| 3 |
(1)f(x)=2cos2x+
sin2x=
sin2x+cos2x+1=2sin(2x+
)+1,
∴周期T=π.
(2)f(A)=2,即sin(2A+
)=
,A=
,
∵a2=b2+c2-2bccosA=b2+c2-bc,
∴b2+c2-bc=3,
又b2+c2+2bc=9,∴bc=2,b+c=3,b>c,解得
.
| 3 |
| 3 |
| π |
| 6 |
∴周期T=π.
(2)f(A)=2,即sin(2A+
| π |
| 6 |
| 1 |
| 2 |
| π |
| 3 |
∵a2=b2+c2-2bccosA=b2+c2-bc,
∴b2+c2-bc=3,
又b2+c2+2bc=9,∴bc=2,b+c=3,b>c,解得
|

练习册系列答案
相关题目
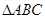 中,角
中,角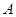 、
、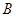 、
、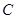 的对边分别为
的对边分别为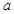 、
、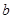 、
、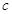 ,且
,且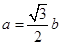 ,
,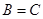 .(1) 求
.(1) 求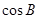 的值;
的值;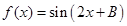 ,求
,求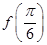 的值.
的值. 中,底面是以
中,底面是以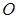 为中心的菱形,
为中心的菱形, 底面
底面 ,
,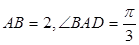 ,
,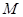 为
为 上一点,且
上一点,且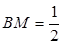 .
.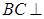 平面
平面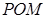 ;
; ,求四棱锥
,求四棱锥 的体积.
的体积.
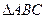 的三内角
的三内角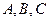 所对边的长分别为
所对边的长分别为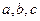 ,已知
,已知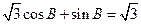 ,
,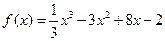 ,
,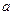 、
、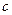 是方程
是方程 的两根,求
的两根,求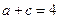 ,求
,求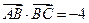 ,求
,求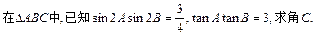
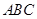 中,
中,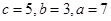 ,则角A的大小为( )
,则角A的大小为( )