题目内容
在锐角△ABC中,a、b、c分别为角A、B、C所对的边,且
=
(Ⅰ)确定角C的大小;
(Ⅱ)若c=
,且△ABC的面积为
,求a2+b2的值.
| a |
| sinA |
| 2c | ||
|
(Ⅰ)确定角C的大小;
(Ⅱ)若c=
| 7 |
3
| ||
| 2 |
(Ⅰ)∵
=
,∴由正弦定理得
=
=
…(2分)
∴sinC=
…(4分)
∵△ABC是锐角三角形,∴C=
…(6分)
(Ⅱ)∵c=
,C=
,△ABC的面积为
,∴由面积公式得
absin
=
…(8分)
∴ab=6…(9分)
由余弦定理得a2+b2-2abcos
=7…(11分)
∴a2+b2=13…(12分)
| a |
| sinA |
| 2c | ||
|
| a |
| sinA |
| c |
| sinC |
| 2c | ||
|
∴sinC=
| ||
| 2 |
∵△ABC是锐角三角形,∴C=
| π |
| 3 |
(Ⅱ)∵c=
| 7 |
| π |
| 3 |
3
| ||
| 2 |
| 1 |
| 2 |
| π |
| 3 |
3
| ||
| 2 |
∴ab=6…(9分)
由余弦定理得a2+b2-2abcos
| π |
| 3 |
∴a2+b2=13…(12分)

练习册系列答案
相关题目
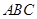 中,内角
中,内角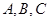 的对边分别为
的对边分别为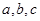 ,已知
,已知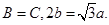
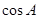 的值;(2)
的值;(2)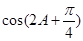 的值.
的值.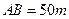 ,
,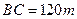 ,于A处测得水深
,于A处测得水深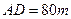 ,于B处测得水深
,于B处测得水深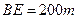 ,于C处测得水深
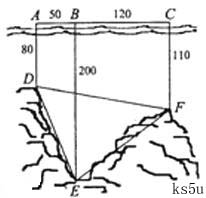
,于C处测得水深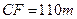 ,求∠DEF的余弦值。
,求∠DEF的余弦值。 

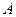 、
、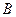 、
、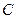 为
为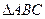 的三个内角,且其对边分别为
的三个内角,且其对边分别为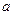 、
、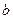 、
、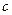 ,若
,若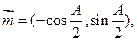
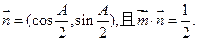
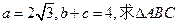 的面积.
的面积.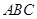 中,若
中,若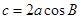 ,则△
,则△ 中,角A、B、C的对边分别是a、b、c,且
中,角A、B、C的对边分别是a、b、c,且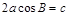 ,则△
,则△