题目内容
△ABC中,a,b,c分别为角A,B,C所对的边,且a=4,b+c=5,tanA+tanB+
=
tanAtanB.
(1)求角C;
(2)求△ABC的面积.
| 3 |
| 3 |
(1)求角C;
(2)求△ABC的面积.
(1)由tanA+tanB+
=
tanAtanB,得tanA+tanB=-
(1-tanAtanB)
=-
,
∴tan(A+B)=
=-
,∵△ABC中,∴A+B=π-C,
∴tan(A+B)=-tanC=-
,tanC=
C=
.
(2)a=4,b+c=5,∵由c2=a2+b2-2abcosCc2=16+(5-c)2-8(5-c)×
,
解得:c=
,b=
,∴S△ABC=
absinC=
×4×
×
=
.
| 3 |
| 3 |
| 3 |
| tanA+tanB |
| 1-tanAtanB |
| 3 |
∴tan(A+B)=
| tanA+tanB |
| 1-tanAtanB |
| 3 |
∴tan(A+B)=-tanC=-
| 3 |
| 3 |
| π |
| 3 |
(2)a=4,b+c=5,∵由c2=a2+b2-2abcosCc2=16+(5-c)2-8(5-c)×
| 1 |
| 2 |
解得:c=
| 7 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| ||
| 2 |
3
| ||
| 2 |

练习册系列答案
相关题目
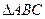 中,
中,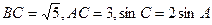
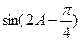 的值。
的值。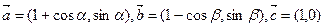 ,
,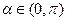 ,
,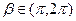 ,向量
,向量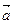 与
与 的夹角为
的夹角为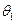 ,向量
,向量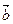 与
与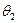 ,且
,且 .若
.若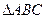 中,角
中,角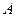 、
、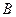 、
、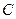 的对边分别为
的对边分别为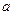 、
、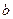 、
、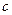 ,且角
,且角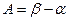 .
.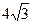 ,试求
,试求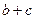 的取值范围.
的取值范围.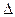 ABC中,
ABC中,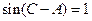 , sinB=
, sinB=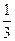 .
.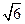 ,求
,求
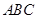 中,角
中,角 所对的边分别为
所对的边分别为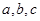 .若
.若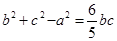 ,则
,则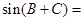 ( )
( )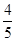

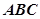 中,角
中,角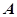 、
、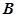 、
、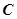 的对边分别为
的对边分别为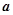 、
、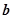 、
、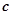 ,且
,且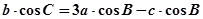 .
.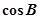 ;
;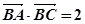 ,且
,且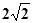 ,求
,求