题目内容
在△ABC中,A=30°,a=1,b=x,如果三角形ABC有两解,则x的取值范围为______.
∵在△ABC中,A=30°,a=1,b=x,
∴由正弦定理
=
得:
=
,
∴sinB=xsin30°=
x,
∴要使三角形ABC有两解,则需b>a,即x>1,且sinB=
x<1(否则为直角三角形或钝角三角形,只有一解),
解得:1<x<2.
∴x的取值范围为(1,2).
故答案为:(1,2).
∴由正弦定理
| a |
| sinA |
| b |
| sinB |
| 1 |
| sin30° |
| x |
| sinB |
∴sinB=xsin30°=
| 1 |
| 2 |
∴要使三角形ABC有两解,则需b>a,即x>1,且sinB=
| 1 |
| 2 |
解得:1<x<2.
∴x的取值范围为(1,2).
故答案为:(1,2).

练习册系列答案
相关题目

 (x≥0),
(x≥0), ,求用
,求用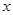 表示
表示 的函数关系式,并求函数的定义域;
的函数关系式,并求函数的定义域;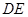 是灌溉水管,为节约成本,希望它最短,
是灌溉水管,为节约成本,希望它最短,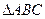 中,若对任意的实数
中,若对任意的实数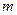 ,有
,有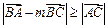 ,则
,则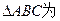 ( )
( )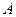 、
、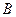 、
、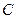 为
为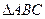 的三个内角,且其对边分别为
的三个内角,且其对边分别为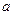 、
、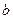 、
、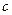 ,若
,若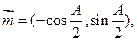
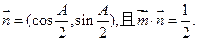
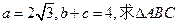 的面积.
的面积.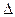 ABC中,
ABC中,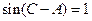 , sinB=
, sinB=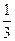 .
.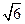 ,求
,求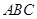 中,若
中,若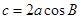 ,则△
,则△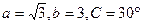 ,则A= 。
,则A= 。