题目内容
15.已知F为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点,a为双曲线虚轴的一个顶点,过点F、A的直线与双曲线的一条渐近线在y轴右侧的交点为B,若$\overrightarrow{AB}$=($\sqrt{2}$-1)$\overrightarrow{AF}$,则此双曲线的离心率是( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | $\sqrt{5}$ |
分析 设F(c,0),A(0,b),渐近线方程为y=$\frac{b}{a}$x,求出AF的方程与y=$\frac{b}{a}$x,联立可得B,利用$\overrightarrow{AB}$=($\sqrt{2}$-1)$\overrightarrow{AF}$,可得a,c的关系,即可求出双曲线的离心率.
解答 解:设F(c,0),A(0,b),渐近线方程为y=$\frac{b}{a}$x,则
直线AF的方程为$\frac{x}{c}+\frac{y}{b}=1$,与y=$\frac{b}{a}$x联立可得B($\frac{ac}{c+a}$,-$\frac{bc}{c+a}$),
∵$\overrightarrow{AB}$=($\sqrt{2}$-1)$\overrightarrow{AF}$,
∴($\frac{ac}{c+a}$,-$\frac{bc}{c+a}$-b)=($\sqrt{2}$-1)(c,-b),
∴c=($\sqrt{2}$+1)$\frac{ac}{c+a}$,
∴e=$\frac{c}{a}$=$\sqrt{2}$,
故选:A.
点评 本题考查双曲线的性质,考查向量知识的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
3.执行如图程序框图,若输出的S值为62,则判断框内为( )
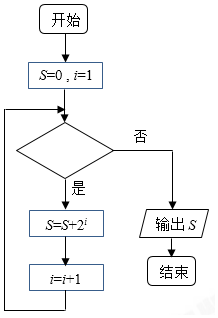

| A. | i≤4? | B. | i≤5? | C. | i≤6? | D. | i≤7? |
7.有一个7人学习合作小组,从中选取4人发言,要求其中组长和副组长至少有一人参加,若组长和副组长同时参加,则他们发言时顺序不能相邻,那么不同的发言顺序有( )
| A. | 720种 | B. | 600种 | C. | 360种 | D. | 300种 |
4.设{an}是等比数列,则对任何n∈N*,都有$\frac{1}{{{a_1}{a_2}}}•\frac{1}{{{a_2}{a_3}}}…\frac{1}{{{a_n}{a_{n+1}}}}$=( )
| A. | $\frac{1}{{{{({a_1}•{a_n})}^n}}}$ | B. | $\frac{1}{{{{({a_1}•{a_{n+1}})}^n}}}$ | C. | $\frac{1}{{{{({a_1}•{a_n})}^{n+1}}}}$ | D. | $\frac{1}{{{{({a_1}•{a_{n+1}})}^{n+1}}}}$ |