题目内容
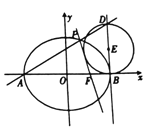
【题目】已知抛物线C:y2=2px(p>0)的焦点F到双曲线 ![]() =1的渐近线的距离为1,过焦点F且斜率为k的直线与抛物线C交于A,B两点,若
=1的渐近线的距离为1,过焦点F且斜率为k的直线与抛物线C交于A,B两点,若 ![]() ,则k= .
,则k= .
【答案】![]()
【解析】解:抛物线C:y2=2px(p>0)的焦点为F( ![]() ,0),
,0),
且F到双曲线 ![]() =1的渐近线y=±
=1的渐近线y=± ![]() x的距离为1,
x的距离为1,
即渐近线的方程为 ![]() x﹣3y=0,
x﹣3y=0,
∴d= ![]() =1,
=1,
解得p=4;即焦点坐标F(2,0),
∴过焦点F斜率为k的直线为y=k(x﹣2),
与抛物线C:y2=8x联立,消去x,得y2=8( ![]() +2),
+2),
整理,得ky2﹣8y﹣16k=0,
解得y= ![]() .
.
又∵ ![]() ,
,
∴(4﹣xA , ﹣yA)=2(xB﹣4,yB),
∴yA=﹣2yB;
当k>0时,yA>0,yB<0,
∴ ![]() =2(﹣
=2(﹣ ![]() ),
),
解得k=2 ![]() ;
;
当k<0时,yA<0,yB>0,
∴﹣ ![]() =2
=2 ![]() ,
,
解得k=﹣2 ![]() ;
;
∴k= ![]() .
.
所以答案是: ![]() .
.

 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案【题目】 某厂生产不同规格的一种产品,根据检测标准,其合格产品的质量![]() 与尺寸
与尺寸![]() 之间近似满足关系式
之间近似满足关系式![]() (
(![]() 为大于
为大于![]() 的常数),现随机抽取
的常数),现随机抽取![]() 件合格产品,测得数据如下:
件合格产品,测得数据如下:
尺寸 |
|
|
|
|
|
|
质量 |
|
|
|
|
|
|
对数据作了初步处理,相关统计量的值如下表:
|
|
|
|
|
|
|
|
(1)根据所给数据,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)按照某项指标测定,当产品质量与尺寸的比在区间![]() 内时为优等品,现从抽取的
内时为优等品,现从抽取的![]() 件合格产品中再任选
件合格产品中再任选![]() 件,记
件,记![]() 为取到优等品的件数,试求随机变量
为取到优等品的件数,试求随机变量![]() 的分布列和期望.
的分布列和期望.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 .
.
【题目】为了解患肺心病是否与性别有关,在某医院对入院者用简单随机抽样方法抽取50人进行调查,结果如下列联表:

(Ⅰ)是否有![]() 的把握认为入院者中患肺心病与性别有关?请说明理由;
的把握认为入院者中患肺心病与性别有关?请说明理由;
(Ⅱ)已知在患肺心病的10位女性中,有3位患胃病.现在从这10位女性中,随机选出3名进行其它方面的排查,记选出患胃病的女性人数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 .
.