题目内容
4.已知正数a,b满足2a2+b2=3,求a$\sqrt{{b}^{2}+1}$的最大值.分析 由题意和基本不等式可得a$\sqrt{{b}^{2}+1}$=$\frac{\sqrt{2}}{2}$•$\sqrt{2}$a•$\sqrt{{b}^{2}+1}$≤$\frac{\sqrt{2}}{2}$•$\frac{(\sqrt{2}a)^{2}+(\sqrt{{b}^{2}+1})^{2}}{2}$,代值计算注意等号成立的条件可得.
解答 解:∵正数a,b满足2a2+b2=3,
∴a$\sqrt{{b}^{2}+1}$=$\frac{\sqrt{2}}{2}$•$\sqrt{2}$a•$\sqrt{{b}^{2}+1}$
≤$\frac{\sqrt{2}}{2}$•$\frac{(\sqrt{2}a)^{2}+(\sqrt{{b}^{2}+1})^{2}}{2}$
=$\frac{\sqrt{2}}{4}$(2a2+b2+1)=$\sqrt{2}$
当且仅当$\sqrt{2}$a=$\sqrt{{b}^{2}+1}$即a=b=1时取等号.
∴a$\sqrt{{b}^{2}+1}$的最大值为$\sqrt{2}$.
点评 本题考查基本不等式求最值,凑出可以基本不等式的形式是解决问题的关键,属基础题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
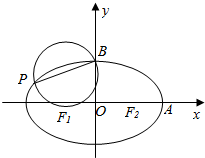 设椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点为F1,F2,右顶点为A,上顶点为B.已知|AB|=$\frac{\sqrt{3}}{2}$|F1F2|.
设椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点为F1,F2,右顶点为A,上顶点为B.已知|AB|=$\frac{\sqrt{3}}{2}$|F1F2|.