题目内容
16.已知两圆C1:(x+5)2+y2=4,C2:(x-5)2+y2=4,动圆C与圆C1外切,而与圆C2内切,求动圆圆心C的轨迹方程.分析 设动圆圆心M(x,y),半径为r,则|MC1|=r+2,|MC2|=r-2,可得|MC1|-|MC2|=r+2-r+2=4<|C1C2|=10,利用双曲线的定义,即可求动圆圆心M的轨迹方程.
解答 解:设动圆圆心M的坐标为(x,y),半径为r,则|MC1|=r+2,|MC2|=r-2,
∴|MC1|-|MC2|=r+2-r+2=4<|C1C2|=10,
由双曲线的定义知,点M的轨迹是以C1、C2为焦点的双曲线的右支,且2a=4,a=2,b=$\sqrt{21}$,
双曲线的方程为:$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{21}=1$(x>0).
点评 本题考查圆与圆的位置关系,考查双曲线的定义,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
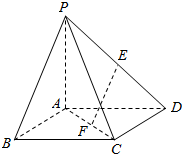 如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PA⊥底面ABCD,PA=AD=1,E、F分别为PD、AC上的动点,且$\frac{DE}{DP}$=$\frac{CF}{CA}$=λ(0<λ<1).
如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PA⊥底面ABCD,PA=AD=1,E、F分别为PD、AC上的动点,且$\frac{DE}{DP}$=$\frac{CF}{CA}$=λ(0<λ<1).