题目内容
【题目】已知函数f(x)=![]() ,x∈[1,+∞).
,x∈[1,+∞).
(1)当a=![]() 时,判断并证明f(x)的单调性;
时,判断并证明f(x)的单调性;
(2)当a=-1时,求函数f(x)的最小值.
【答案】见解析
【解析】 (1)当a=![]() 时,f(x)=
时,f(x)=![]() =x+2+
=x+2+![]() =x+
=x+![]() +2.
+2.
函数f(x)在[1,+∞)上是单调递增函数,证明如下:
设x1,x2是[1,+∞)上的任意两个实数,且x1<x2,
则![]()
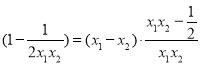 .
.
因为![]() ,所以x1-x2<0,x1·x2>0,x1x2-
,所以x1-x2<0,x1·x2>0,x1x2-![]() >0,
>0,
所以f(x1)-f(x2)<0,即f(x1)<f(x2).
所以函数f(x)在[1,+∞)上是单调递增函数.
(2)当a=-1时,f(x)=x-![]() +2.
+2.
由函数y1=x和y2=-![]() 在[1,+∞)上都是单调递增函数,结合单调性的性质,可得f(x)=x-
在[1,+∞)上都是单调递增函数,结合单调性的性质,可得f(x)=x-![]() +2在[1,+∞)上是单调递增函数.
+2在[1,+∞)上是单调递增函数.
当x=1时,f(x)取得最小值f(1)=1-1+2=2,
故函数f(x)的最小值为2.

练习册系列答案
相关题目