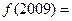题目内容
已知函数
(I)求 在区间
在区间 上的最大值
上的最大值
(II)是否存在实数 使得
使得 的图象与
的图象与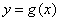 的图象有且只有三个不同的交点?若存在,求出
的图象有且只有三个不同的交点?若存在,求出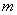 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。

(I)求
 在区间
在区间 上的最大值
上的最大值
(II)是否存在实数
 使得
使得 的图象与
的图象与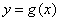 的图象有且只有三个不同的交点?若存在,求出
的图象有且只有三个不同的交点?若存在,求出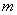 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。:(I)
当 即
即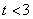 时,
时, 在
在 上单调递增,
上单调递增,
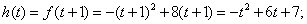
当 即
即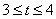 时,
时,
当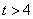 时,
时, 在
在 上单调递减,
上单调递减,
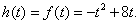
综上,
(II)函数 的图象与
的图象与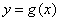 的图象有且只有三个不同的交点,即函数
的图象有且只有三个不同的交点,即函数
 的图象与
的图象与 轴的正半轴有且只有三个不同的交点[.]
轴的正半轴有且只有三个不同的交点[.]

当 时,
时,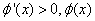 是增函数;
是增函数;
当 时,
时, 是减函数;
是减函数;
当 时,
时,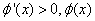 是增函数;
是增函数;
当 或
或 时,
时,
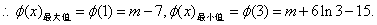
 当
当 充分接近0时,
充分接近0时, 当
当 充分大时,
充分大时,
 要使
要使 的图象与
的图象与 轴正半轴有三个不同的交点,必须且只须
轴正半轴有三个不同的交点,必须且只须
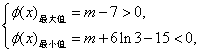 即
即
所以存在实数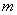 ,使得函数
,使得函数 与
与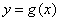 的图象有且只有三个不同的交点,
的图象有且只有三个不同的交点,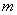 的取值范围为
的取值范围为

当
 即
即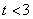 时,
时, 在
在 上单调递增,
上单调递增,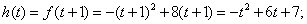
当
 即
即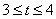 时,
时,
当
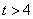 时,
时, 在
在 上单调递减,
上单调递减,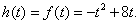
综上,

(II)函数
 的图象与
的图象与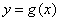 的图象有且只有三个不同的交点,即函数
的图象有且只有三个不同的交点,即函数 的图象与
的图象与 轴的正半轴有且只有三个不同的交点[.]
轴的正半轴有且只有三个不同的交点[.]
当
 时,
时,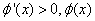 是增函数;
是增函数;当
 时,
时, 是减函数;
是减函数;当
 时,
时,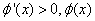 是增函数;
是增函数;当
 或
或 时,
时,
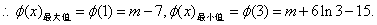
 当
当 充分接近0时,
充分接近0时, 当
当 充分大时,
充分大时,
 要使
要使 的图象与
的图象与 轴正半轴有三个不同的交点,必须且只须
轴正半轴有三个不同的交点,必须且只须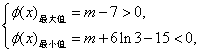 即
即
所以存在实数
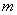 ,使得函数
,使得函数 与
与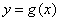 的图象有且只有三个不同的交点,
的图象有且只有三个不同的交点,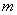 的取值范围为
的取值范围为
本小题主要考查函数的单调性、极值、最值等基本知识,考查运用导数研究函数性质的方法,考查运算能力,考查函数与方程、数形结合、分类与整合等数学思想方法和分析问题、解决问题的能力

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 )
)
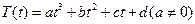 ,其中温度的单位是℃,时间的单位是小时.中午12:00相应的t=0,中午12:00以后相应的t取正数,中午12:00以前相应的t取负数(如早上8:00相应的t=-4,下午16:00相应的t=4).若测得该物体在早上8:00的温度为8℃,中午12:00的温度为60℃,下午13:00的温度为58℃,且已知该物体的温度早上8:00与下午16:00有相同的变化率.
,其中温度的单位是℃,时间的单位是小时.中午12:00相应的t=0,中午12:00以后相应的t取正数,中午12:00以前相应的t取负数(如早上8:00相应的t=-4,下午16:00相应的t=4).若测得该物体在早上8:00的温度为8℃,中午12:00的温度为60℃,下午13:00的温度为58℃,且已知该物体的温度早上8:00与下午16:00有相同的变化率.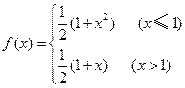 在
在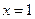 处是否可导.
处是否可导.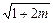 -
-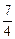 +cos2x)对任意x∈R都成立,求实数m的取值范围.
+cos2x)对任意x∈R都成立,求实数m的取值范围.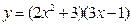 ; (2)
; (2)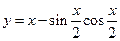 .
.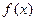 是定义在R上的偶函数,对任意的
是定义在R上的偶函数,对任意的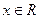 ,都有
,都有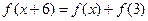 成立,若
成立,若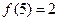 ,则
,则