题目内容
在半径为R的圆内,作内接等腰三角形,当底边上高为_______时它的面积最大.
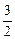 R
R 设圆内接等腰三角形的底边长为2x,高为h,
那么h=AO+BO=R+ ,解得
,解得
x2=h(2R-h),于是内接三角形的面积为
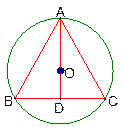
S=x·h=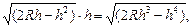
从而
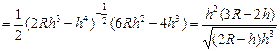
令S′=0,解得h=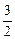 R,由于不考虑不存在的情况,所在区间(0,2R)上列表如下:
R,由于不考虑不存在的情况,所在区间(0,2R)上列表如下:
由此表可知,当x=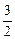 R时,等腰三角形面积最大.
R时,等腰三角形面积最大.
那么h=AO+BO=R+
 ,解得
,解得x2=h(2R-h),于是内接三角形的面积为

S=x·h=
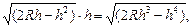
从而

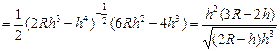
令S′=0,解得h=
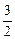 R,由于不考虑不存在的情况,所在区间(0,2R)上列表如下:
R,由于不考虑不存在的情况,所在区间(0,2R)上列表如下:| h | (0,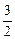 R) R) | 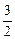 R R | (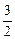 ,2R) ,2R) |
| S′ | + | 0 | - |
| S | 增函数 | 最大值 | 减函数 |
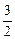 R时,等腰三角形面积最大.
R时,等腰三角形面积最大.
练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
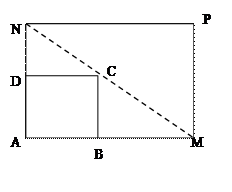 (Ⅱ)若AN的长度不小于6米,则当AM、AN的长度是多少时,矩形AMPN的面积最小并求出最小面积.
(Ⅱ)若AN的长度不小于6米,则当AM、AN的长度是多少时,矩形AMPN的面积最小并求出最小面积. 型电脑.1993年这种电脑每台平均生产成本为5000元,并以纯利润
型电脑.1993年这种电脑每台平均生产成本为5000元,并以纯利润 确定出厂价.从1994年开始,公司通过更新设备和加强管理,使生产成本逐年降低.到1997年,尽管
确定出厂价.从1994年开始,公司通过更新设备和加强管理,使生产成本逐年降低.到1997年,尽管 ,但却实现了
,但却实现了 纯利润的高效益.
纯利润的高效益. ,以下数据可供参考:
,以下数据可供参考: ,
, ).
).
 在区间
在区间 上的最大值
上的最大值
 使得
使得 的图象与
的图象与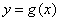 的图象有且只有三个不同的交点?若存在,求出
的图象有且只有三个不同的交点?若存在,求出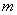 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。 ,f2(x)=x+2,
,f2(x)=x+2, ,试画出y=f(x)的图像并求y=f(x)的曲线绕x轴旋转一周所得几何体的表面积;
,试画出y=f(x)的图像并求y=f(x)的曲线绕x轴旋转一周所得几何体的表面积; ],求b的值.
],求b的值. 




 时整,甲船自
时整,甲船自 处以
处以 的速度向正东行驶,乙船自
的速度向正东行驶,乙船自 处以
处以 分时两船之间距离对时间的变化率是_____________.
分时两船之间距离对时间的变化率是_____________. 在x0到x0+Δx之间的平均变化率.
在x0到x0+Δx之间的平均变化率.