题目内容
设m是实数,记M={m|m>1},f(x)=log3(x2-4mx+4m2+m+ )
)
(1)证明: 当m∈M时,f(x)对所有实数都有意义;反之,若f(x)对所有实数x都有意义,则m∈M。
(2)当m∈M时,求函数f(x)的最小值。
(3)求证: 对每个m∈M,函数f(x)的最小值都不小于1。
 )
)
(1)证明: 当m∈M时,f(x)对所有实数都有意义;反之,若f(x)对所有实数x都有意义,则m∈M。
(2)当m∈M时,求函数f(x)的最小值。
(3)求证: 对每个m∈M,函数f(x)的最小值都不小于1。
(1) 证明略(2) 当x=m时, f(2m)=log3(m+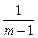 )为最小值。
)为最小值。
(3)证明略
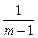 )为最小值。
)为最小值。(3)证明略
先将f(x)变形: f(x)=log3[(x-2m)2+m+ ],
],
当m∈M时,m>1,∴(x-m)2+m+ >0恒成立,
>0恒成立,
故f(x)的定义域为R。
反之,若f(x)对所有实数x都有意义,则只须x2-4mx+4m2+m+ >0,令Δ<0,即16m2-4(4m2+m+
>0,令Δ<0,即16m2-4(4m2+m+ )<0,解得m>1,故m∈M。
)<0,解得m>1,故m∈M。
(2)解析: 设u=x2-4mx+4m2+m+ ,
,
∵y=log3u是增函数,∴当u最小时,f(x)最小。
而u=(x-2m)2+m+ ,
,
显然,当x=m时,u取最小值为m+ ,
,
此时f(2m)=log3(m+ )为最小值。
)为最小值。
(3)证明: 当m∈M时,m+ =(m-1)+
=(m-1)+  +1≥3,
+1≥3,
当且仅当m=2时等号成立。
∴log3(m+ )≥log33=1。
)≥log33=1。
 ],
],当m∈M时,m>1,∴(x-m)2+m+
 >0恒成立,
>0恒成立,故f(x)的定义域为R。
反之,若f(x)对所有实数x都有意义,则只须x2-4mx+4m2+m+
 >0,令Δ<0,即16m2-4(4m2+m+
>0,令Δ<0,即16m2-4(4m2+m+ )<0,解得m>1,故m∈M。
)<0,解得m>1,故m∈M。(2)解析: 设u=x2-4mx+4m2+m+
 ,
,∵y=log3u是增函数,∴当u最小时,f(x)最小。
而u=(x-2m)2+m+
 ,
,显然,当x=m时,u取最小值为m+
 ,
,此时f(2m)=log3(m+
 )为最小值。
)为最小值。(3)证明: 当m∈M时,m+
 =(m-1)+
=(m-1)+  +1≥3,
+1≥3,当且仅当m=2时等号成立。
∴log3(m+
 )≥log33=1。
)≥log33=1。 
练习册系列答案
相关题目
 ,其中
,其中 .
. 在点
在点 处的切线方程为
处的切线方程为 ,求函数
,求函数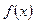 的解析式;
的解析式; +1上一点(-1,0),且与曲线在该点处的切线垂直的直线方程是( )
+1上一点(-1,0),且与曲线在该点处的切线垂直的直线方程是( ) +3 C y=-
+3 C y=- D y=-3x-3
D y=-3x-3
 在区间
在区间 上的最大值
上的最大值
 使得
使得 的图象与
的图象与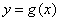 的图象有且只有三个不同的交点?若存在,求出
的图象有且只有三个不同的交点?若存在,求出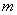 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。




 ,则f(2009)的值为( )
,则f(2009)的值为( )