题目内容
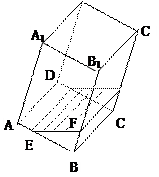
如图, PA⊥平面ABCD,四边形ABCD是矩形,点E在边AB上,F为PD的中点,AF∥平面PCE,二面角P-CD-B为450,AD=2,CD=3.
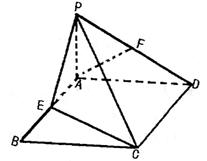
(1)试确定E点位置; (2)求直线AF到平面PCE的距离.

(1)试确定E点位置; (2)求直线AF到平面PCE的距离.
(1)过AF、AB作平面β交PC于点G,连FG、EG,
∵四边形ABCD是矩形,点E在边AB上,∴EA∥CD,
∴EA∥平面PCD, ∴EA∥FG∥CD,
∵AF∥平面PCE,∴AF∥EG, 则四边形AEGF是平行四边形
又∵F为PD的中点,∴EA=FG=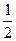 CD,
CD,
则点E是边AB的中点.
(2)延长CE、DA交于点H,作AM⊥HC,垂足为点M;连接AM、PM,作AN ⊥PM,垂足为点N.∵PA⊥平面ABCD,∴PA⊥HC,则HC⊥平面PAM,
∴HC⊥AN,则AN ⊥平面PEC;又∵AF∥平面PCE,∴线段AN的长是直线AF到平面PCE的距离. ∵二面角P-CD-B为450,可证得∠PAD就是二面角P-CD-B的平面角,
∴∠PAD=450. 在Rt△PAD中,∵AD=2,∴PA="2."
又在Rt△HCD中,∵EA =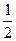 CD,CD=3,∴AH= AD=2.
CD,CD=3,∴AH= AD=2.
∵AM⊥HC,∴Rt△HCD∽Rt△HAM,可求得AM=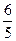 .
.
在Rt△PAM中,∵S△PAM=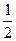 PA•AM=
PA•AM=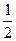 AN•PM,∴AN=
AN•PM,∴AN=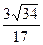 .
.
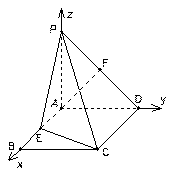
解法二:以点A为原点,分别以AB、AD、AP所在直线为X、Y、Z轴,建立空间直角坐标系(如图所示),由已知可得A(0,0,0),B(3,0,0),D(0,2,0),C(3,2,0),
∵二面角P-CD-B为450,可证得∠PAD就是二面角P-CD-B的平面角,∴∠PAD=450.
在Rt△PAD中, AD=2,∴PA=2,则P(0,0,2)
又∵F为PD的中点,∴F(0,1,1)
则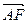 =(0,1,1),
=(0,1,1),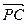 =(3,2,-2)
=(3,2,-2)
∵点E在边AB上,∴设E(λ,0,0),
则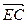 =(3-λ,2,0)
=(3-λ,2,0)
设平面PEC的法向量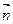 =(x,y,z),由
=(x,y,z),由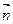 •
•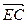 =0得(3-λ)x+2y=0,
=0得(3-λ)x+2y=0,
由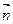 •
•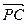 =0得3x+2y-2z=0,解得y=
=0得3x+2y-2z=0,解得y=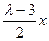 ,z=
,z= ;
;
令x=2,得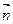 =(2,λ-3,λ)
=(2,λ-3,λ)
(1)∵AF∥平面PCE,∴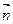 •
•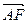 =0,即λ-3+λ=0,∴λ=
=0,即λ-3+λ=0,∴λ=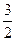
则点E是边AB的中点.
(2)∵AF∥平面PCE,∴直线AF到平面PCE的距离等于点A到平面PCE的距离d,则d= =
=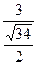 =
=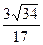

∵四边形ABCD是矩形,点E在边AB上,∴EA∥CD,
∴EA∥平面PCD, ∴EA∥FG∥CD,
∵AF∥平面PCE,∴AF∥EG, 则四边形AEGF是平行四边形
又∵F为PD的中点,∴EA=FG=
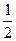 CD,
CD,则点E是边AB的中点.
(2)延长CE、DA交于点H,作AM⊥HC,垂足为点M;连接AM、PM,作AN ⊥PM,垂足为点N.∵PA⊥平面ABCD,∴PA⊥HC,则HC⊥平面PAM,
∴HC⊥AN,则AN ⊥平面PEC;又∵AF∥平面PCE,∴线段AN的长是直线AF到平面PCE的距离. ∵二面角P-CD-B为450,可证得∠PAD就是二面角P-CD-B的平面角,
∴∠PAD=450. 在Rt△PAD中,∵AD=2,∴PA="2."
又在Rt△HCD中,∵EA =
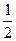 CD,CD=3,∴AH= AD=2.
CD,CD=3,∴AH= AD=2.∵AM⊥HC,∴Rt△HCD∽Rt△HAM,可求得AM=
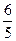 .
. 在Rt△PAM中,∵S△PAM=
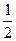 PA•AM=
PA•AM=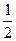 AN•PM,∴AN=
AN•PM,∴AN=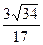 .
. 解法二:以点A为原点,分别以AB、AD、AP所在直线为X、Y、Z轴,建立空间直角坐标系(如图所示),由已知可得A(0,0,0),B(3,0,0),D(0,2,0),C(3,2,0),
∵二面角P-CD-B为450,可证得∠PAD就是二面角P-CD-B的平面角,∴∠PAD=450.
在Rt△PAD中, AD=2,∴PA=2,则P(0,0,2)
又∵F为PD的中点,∴F(0,1,1)
则
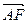 =(0,1,1),
=(0,1,1),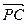 =(3,2,-2)
=(3,2,-2) ∵点E在边AB上,∴设E(λ,0,0),
则
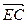 =(3-λ,2,0)
=(3-λ,2,0)设平面PEC的法向量
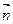 =(x,y,z),由
=(x,y,z),由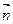 •
•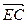 =0得(3-λ)x+2y=0,
=0得(3-λ)x+2y=0,由
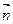 •
•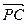 =0得3x+2y-2z=0,解得y=
=0得3x+2y-2z=0,解得y=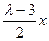 ,z=
,z= ;
;令x=2,得
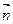 =(2,λ-3,λ)
=(2,λ-3,λ) (1)∵AF∥平面PCE,∴
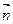 •
•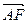 =0,即λ-3+λ=0,∴λ=
=0,即λ-3+λ=0,∴λ=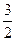
则点E是边AB的中点.
(2)∵AF∥平面PCE,∴直线AF到平面PCE的距离等于点A到平面PCE的距离d,则d=
 =
=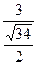 =
=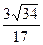
略

练习册系列答案
相关题目


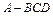 中,三条棱
中,三条棱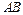 、
、 、
、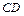 两两垂直,且
两两垂直,且 与平面
与平面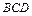 成
成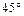 角,与平面
角,与平面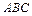 成
成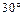 角.
角.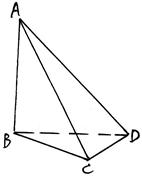
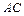 与平面
与平面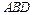 所成角的大小;
所成角的大小;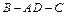 大小的余弦值.
大小的余弦值.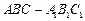 的底面是直角三角形,
的底面是直角三角形, ,侧棱与底面所成的角为
,侧棱与底面所成的角为 ,点
,点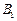 在底面上的射影
在底面上的射影 落在
落在 上.
上.
 ,求
,求 的值.
的值. ,且当
,且当 时,求二面角
时,求二面角 的大小.
的大小. 中.
中.
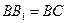 ,
,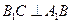 ,证明:平面
,证明:平面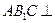 平面
平面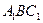 ;
;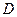 是
是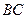 的中点,
的中点,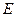 是
是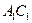 上的一点,
上的一点,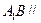 平面
平面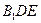 ,求
,求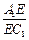 的值.
的值.
 平方米的材料制成一个有盖的圆锥形容器,如果在制作过程中材料无损耗,且材料的厚度忽略不计,底面半径长为
平方米的材料制成一个有盖的圆锥形容器,如果在制作过程中材料无损耗,且材料的厚度忽略不计,底面半径长为 ,圆锥母线的长为
,圆锥母线的长为

 ,求所制作的圆锥形容器容积多少立方米(精确到0. 01m3) (6分)
,求所制作的圆锥形容器容积多少立方米(精确到0. 01m3) (6分)