题目内容
14. 如图点O在△ABC外部(O,A在直线BC的异侧),△ABC与△OBC的面积之比为1:3;记$\overrightarrow{AO}$=λ1$\overrightarrow{AB}$+λ2$\overrightarrow{AC}$,则λ12+λ22的最小值为( )
如图点O在△ABC外部(O,A在直线BC的异侧),△ABC与△OBC的面积之比为1:3;记$\overrightarrow{AO}$=λ1$\overrightarrow{AB}$+λ2$\overrightarrow{AC}$,则λ12+λ22的最小值为( )| A. | 16 | B. | $\frac{16}{9}$ | C. | 8 | D. | $\frac{8}{9}$ |
分析 设AO和BC的交点为P,推出$\overrightarrow{AP}$=t$\overrightarrow{AB}$+(1-t)$\overline{AC}$,利用三角形的面积推出:$\overrightarrow{AP}$=$\frac{1}{4}$$\overrightarrow{AO}$,求出λ1+λ2=4,利用基本不等式求解最值.
解答 解:设AO和BC的交点为P,则$\overrightarrow{AP}$=t$\overrightarrow{AB}$+(1-t)$\overline{AC}$,
又$\overrightarrow{AO}$=λ1$\overrightarrow{AB}$+λ2$\overrightarrow{AC}$,
根据题意,△ABC与△OBC的面积之比为1:3;
$\overrightarrow{AP}$=$\frac{1}{4}$$\overrightarrow{AO}$,
∴t$\overrightarrow{AB}$+(1-t)$\overline{AC}$=$\frac{1}{4}$λ1$\overrightarrow{AB}$+$\frac{1}{4}$λ2$\overrightarrow{AC}$,
∴$\left\{\begin{array}{l}{t=\frac{1}{4}{λ}_{1}}\\{1-t=\frac{1}{4}{λ}_{2}}\end{array}\right.$,
∴λ1+λ2=4,则λ12+λ22≥$\frac{({λ}_{1}+{λ}_{2})^{2}}{2}$=8.当且仅当λ1=λ2=2时取等号.
故选:C.
点评 本题考查向量在几何中的应用,基本不等式的应用,考查转化思想以及计算能力.

练习册系列答案
相关题目
4.已知全集U=R,集合A={x|$\frac{x+1}{x-1}$≥0},B={x||2x-1|≥1},则B∩∁UA等于( )
| A. | {x|-1<x≤0} | B. | {x|0≤x<1} | C. | {x|-1<x≤0,或x=1} | D. | {x|0≤x<1,或x=-1} |
5.设常数a∈R,集合A={x|x2-(a+1)x+a≥0},B={x|x≥a-1},若A∪B=R,则a的取值范围是( )
| A. | (-∞,2) | B. | (-∞,2] | C. | (2,+∞) | D. | [2,+∞) |
19.高一(1)班进行的演讲比赛中,共有6位选手参加,其中4位女生,2位男生,如果2位男生不能连续出场,且女生甲不能排在第一个,则6位选手出场顺序的排法种数为( )
| A. | 320 | B. | 384 | C. | 408 | D. | 480 |
6.某算法程序如图所示,执行该程序,若输入4,则输出的S为( )
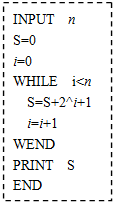
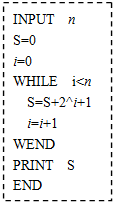
| A. | 36 | B. | 19 | C. | 16 | D. | 10 |
3.若纯虚数(a+i)2(i为虚数单位)在复平面内对应的点在直线x-y+1=0的下方,则实数a的值是( )
| A. | -1 | B. | 1 | C. | -$\sqrt{2}$ | D. | $\sqrt{2}$ |
4.已知过双曲线x2-y2=2的左焦点作直线l与双曲线交于A,B两点.且|AB|=4,则这样的直线有( )
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
