题目内容
11.设平面向量$\overrightarrow m=(cosα,sinα)$(0≤α<2π),$\overrightarrow n=(-\frac{1}{2},\frac{{\sqrt{3}}}{2})$(1)证明;$(\overrightarrow m+\overrightarrow n)⊥(\overrightarrow m-\overrightarrow n)$
(2)当$|{\sqrt{3}\overrightarrow m+\overrightarrow n}|=|{\overrightarrow m-\sqrt{3}\overrightarrow n}$|,求α.
分析 (1)根据向量$\overrightarrow{m},\overrightarrow{n}$的坐标即可求出$(\overrightarrow{m}+\overrightarrow{n})•(\overrightarrow{m}-\overrightarrow{n})={\overrightarrow{m}}^{2}-{\overrightarrow{n}}^{2}=0$,从而便得到$(\overrightarrow{m}+\overrightarrow{n})⊥(\overrightarrow{m}-\overrightarrow{n})$;
(2)对$|\sqrt{3}\overrightarrow{m}+\overrightarrow{n}|=|\overrightarrow{m}-\sqrt{3}\overrightarrow{n}|$两边平方,从而可得到$-\frac{1}{2}cosα+\frac{\sqrt{3}}{2}sinα=0$,进一步得到$sin(α-\frac{π}{6})=0$,根据α的范围求出$α-\frac{π}{6}$的范围,从而得到α的范围.
解答 解:(1)由条件:$(\overrightarrow{m}+\overrightarrow{n})•(\overrightarrow{m}-\overrightarrow{n})={\overrightarrow{m}}^{2}-{\overrightarrow{n}}^{2}$=$(co{s}^{2}α+si{n}^{2}α)-(\frac{1}{4}+\frac{3}{4})=0$;
∴$(\overrightarrow{m}+\overrightarrow{n})⊥(\overrightarrow{m}-\overrightarrow{n})$;
(2)对$|\sqrt{3}\overrightarrow{m}+\overrightarrow{n}|=|\overrightarrow{m}-\sqrt{3}\overrightarrow{n}|$两边平方得:
$3{\overrightarrow{m}}^{2}+2\sqrt{3}\overrightarrow{m}•\overrightarrow{n}+{\overrightarrow{n}}^{2}$=${\overrightarrow{m}}^{2}-2\sqrt{3}\overrightarrow{m}•\overrightarrow{n}+3{\overrightarrow{n}}^{2}$;
∴$3+2\sqrt{3}\overrightarrow{m}•\overrightarrow{n}+1=1-2\sqrt{3}\overrightarrow{m}•\overrightarrow{n}+3$;
∴$\overrightarrow{m}•\overrightarrow{n}=0$;
即$-\frac{1}{2}cosα+\frac{\sqrt{3}}{2}sinα=sin(α-\frac{π}{6})=0$;
∵0≤α<2π;
∴$-\frac{π}{6}≤α-\frac{π}{6}<\frac{11π}{6}$;
∴$α-\frac{π}{6}=0,或π$;
∴$α=\frac{π}{6}$,或$\frac{7π}{6}$.
点评 考查向量数量积的坐标运算,向量垂直的充要条件,以及两角差的正弦公式,注意α的范围.

 小学教材完全解读系列答案
小学教材完全解读系列答案| A. | $\frac{1}{6}$ | B. | $\frac{5}{12}$ | C. | $\frac{7}{12}$ | D. | $\frac{1}{3}$ |
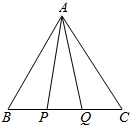 如图,在边长为6的正三角形△ABC内,△APQ的边PQ在BC边上滑动且PQ=2,求△APQ三边的平方和的最大值与最小值.
如图,在边长为6的正三角形△ABC内,△APQ的边PQ在BC边上滑动且PQ=2,求△APQ三边的平方和的最大值与最小值. 如图所示,一海轮在海上A处以每小时80海里的速度沿着南偏东40°的方向航行,这时观测到灯塔B在南偏东70°的方向上,航行1小时到达C处,在C处观测到灯塔B在北偏东65°方向上,问这时C到灯塔B的距离是多少?
如图所示,一海轮在海上A处以每小时80海里的速度沿着南偏东40°的方向航行,这时观测到灯塔B在南偏东70°的方向上,航行1小时到达C处,在C处观测到灯塔B在北偏东65°方向上,问这时C到灯塔B的距离是多少?