题目内容
10.解不等式x6+x5+x3+x-1≤0.分析 对应方程可化为(x3-$\frac{1}{{x}^{3}}$)+(x2+$\frac{1}{{x}^{2}}$)+1=0,换元令x-$\frac{1}{x}$=t,解不等式可得t=x-$\frac{1}{x}$≤-1,再解关于x的不等式可得.
解答 解:研究方程x6+x5+x3+x-1=0的根的情况,
显然x=0不是方程的根,
故在方程x6+x5+x3+x-1=0的两边同除以x3,
则方程可化为(x3-$\frac{1}{{x}^{3}}$)+(x2+$\frac{1}{{x}^{2}}$)+1=0,
令x-$\frac{1}{x}$=t,则方程可化为t3+3t+t2+3=0,
因式分解可得(t+1)(t2+3)=0,
解得t=-1,故不等式的解集为t=x-$\frac{1}{x}$≤-1,
解得$\frac{-1-\sqrt{5}}{2}$≤x≤$\frac{-1+\sqrt{5}}{2}$
∴原不等式的解集为{x|$\frac{-1-\sqrt{5}}{2}$≤x≤$\frac{-1+\sqrt{5}}{2}$}
点评 本题考查高次不等式的解集,换元法是解决问题的关键,属中档题.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
14.已知函数f(x)=|x+a|在区间(-∞,1]上单调递减,则a的取值范围是( )
| A. | a≥1 | B. | 0<a≤1 | C. | a≤-1 | D. | -1≤a<0 |
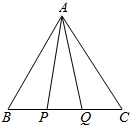 如图,在边长为6的正三角形△ABC内,△APQ的边PQ在BC边上滑动且PQ=2,求△APQ三边的平方和的最大值与最小值.
如图,在边长为6的正三角形△ABC内,△APQ的边PQ在BC边上滑动且PQ=2,求△APQ三边的平方和的最大值与最小值. 如图所示,一海轮在海上A处以每小时80海里的速度沿着南偏东40°的方向航行,这时观测到灯塔B在南偏东70°的方向上,航行1小时到达C处,在C处观测到灯塔B在北偏东65°方向上,问这时C到灯塔B的距离是多少?
如图所示,一海轮在海上A处以每小时80海里的速度沿着南偏东40°的方向航行,这时观测到灯塔B在南偏东70°的方向上,航行1小时到达C处,在C处观测到灯塔B在北偏东65°方向上,问这时C到灯塔B的距离是多少?