题目内容
14.在△ABC中,已知b=5,c=4$\sqrt{2}$,cos(C-B)=$\frac{7\sqrt{2}}{10}$,则cosA=$\frac{8\sqrt{10}-7\sqrt{2}}{10}$.分析 如图所示:根据cosBcosC=$\frac{m}{4\sqrt{2}}$•$\frac{n}{5}$=$\frac{1}{2}$[cos(C-B)+cos(C+B)]=$\frac{1}{2}$[$\frac{7\sqrt{2}}{10}$-cosA],再由cosA=cosαcosβ-sinαsinβ═$\frac{{h}^{2}}{4\sqrt{10}}$-$\frac{1}{2}$($\frac{7\sqrt{2}}{10}$-cosA),求得cosA=$\frac{{h}^{2}}{2\sqrt{10}}$-$\frac{7\sqrt{2}}{10}$.再根据cos(C-B)=cos(C-B)=cosCcosB+sinCsinB=$\frac{m}{4\sqrt{2}}$•$\frac{n}{5}$+$\frac{h}{5}$•$\frac{h}{4\sqrt{2}}$=$\frac{7\sqrt{2}}{10}$,以及 ${(4\sqrt{2})}^{2}$-m2=52-n2 =h2,求得m和h2的值,可得cosA的值.
解答  解:在△ABC中,已知b=6,c=5,cos(C-B)=$\frac{7\sqrt{2}}{10}$,
解:在△ABC中,已知b=6,c=5,cos(C-B)=$\frac{7\sqrt{2}}{10}$,
作AD⊥BC,D为垂足.
设BD=m,CD=n,AD=h,∠BAD=α,∠CAD=β,如图所示:
则cosBcosC=$\frac{m}{4\sqrt{2}}$•$\frac{n}{5}$,
又cosBcosC=$\frac{1}{2}$[cos(C-B)+cos(C+B)]=$\frac{1}{2}$($\frac{7\sqrt{2}}{10}$-cosA),
∴$\frac{m}{4\sqrt{2}}$•$\frac{n}{5}$=$\frac{1}{2}$($\frac{7\sqrt{2}}{10}$-cosA).
∴cosA=cos(α+β)=cosαcosβ-sinαsinβ=$\frac{h}{4\sqrt{2}}$•$\frac{h}{\sqrt{5}}$-$\frac{m}{4\sqrt{2}}$•$\frac{n}{5}$=$\frac{{h}^{2}}{4\sqrt{10}}$-$\frac{mn}{4\sqrt{10}}$=$\frac{{h}^{2}}{4\sqrt{10}}$-$\frac{1}{2}$($\frac{7\sqrt{2}}{10}$-cosA),
∴cosA=$\frac{{h}^{2}}{2\sqrt{10}}$-$\frac{7\sqrt{2}}{10}$.
∵cos(C-B)=cosCcosB+sinCsinB=$\frac{m}{4\sqrt{2}}$•$\frac{n}{5}$+$\frac{h}{5}$•$\frac{h}{4\sqrt{2}}$=$\frac{7\sqrt{2}}{10}$,${(4\sqrt{2})}^{2}$-m2=52-n2 =h2,
解得m=4,h2=16,∴cosA=$\frac{16}{2\sqrt{10}}$-$\frac{7\sqrt{2}}{10}$=$\frac{8\sqrt{10}-7\sqrt{2}}{10}$.
点评 本题主要考查两角和差的三角公式、直角三角形中的边角关系,体现了数形结合的数学思想,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案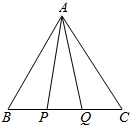 如图,在边长为6的正三角形△ABC内,△APQ的边PQ在BC边上滑动且PQ=2,求△APQ三边的平方和的最大值与最小值.
如图,在边长为6的正三角形△ABC内,△APQ的边PQ在BC边上滑动且PQ=2,求△APQ三边的平方和的最大值与最小值.