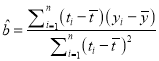题目内容
【题目】已知圆O：x2+y2=2，直线．l：y=kx-2．
（1）若直线l与圆O相切，求k的值；
（2）若直线l与圆O交于不同的两点A，B，当∠AOB为锐角时，求k的取值范围；
（3）若
，P是直线l上的动点，过P作圆O的两条切线PC，PD，切点为C，D，探究：直线CD是否过定点．
【答案】（1）k=±1；（2）（-
）∪（1，
）；（3）直线CD过定点（
）．
【解析】
（1）由直线l与圆O相切，得圆心O（0，0）到直线l的距离等于半径r=
，由此能求出k．
（2）设A，B的坐标分别为（x1，y1），（x2，y2），将直线l：y=kx-2代入x2+y2=2，得（1+k2）x2-4kx+2=0，由此利用根的判断式、向量的数量积公式能求出k的取值范围．
（3）由题意知O，P，C，D四点共圆且在以OP为直径的圆上，设P（t，
），其方程为
，C，D在圆O：x2+y2=2上，求出直线CD：（x+
）t-2y-2=0，联立方程组能求出直线CD过定点（
）．
解：（1）∵圆O：x2+y2=2，直线l：y=kx-2．直线l与圆O相切，
∴圆心O（0，0）到直线l的距离等于半径r=，
即d=
=，
解得k=±1．
（2）设A，B的坐标分别为（x1，y1），（x2，y2），
将直线l：y=kx-2代入x2+y2=2，整理，得（1+k2）x2-4kx+2=0，
∴
，
，
△=（-4k）2-8（1+k2）＞0，即k2＞1，
当∠AOB为锐角时，
=x1x2+y1y2=x1x2+（kx1-2）（kx2-2）
=
=
＞0，
解得k2＜3，
又k2＞1，∴-
或1＜k＜
．
故k的取值范围为（-
）∪（1，）．
（3）由题意知O，P，C，D四点共圆且在以OP为直径的圆上，
设P（t，
），其方程为x（x-t）+y（y
）=0，
∴
，
又C，D在圆O：x2+y2=2上，
两圆作差得lCD：tx+
，即（x+
）t-2y-2=0，
由
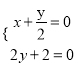，得
，
∴直线CD过定点（
）．
