题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的极小值;
的极小值;
(2)若![]() 上,使得
上,使得![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
【答案】(1)2;(2)  .
.
【解析】试题分析:(1)将参数值代入表达式,再进行求导,根据导函数的正负得到原函数的单调性,进而得到极值;(2)![]() ,有解,即h(x)的最小值小于0即可,对函数求导,研究函数的单调性,得到最小值即可.
,有解,即h(x)的最小值小于0即可,对函数求导,研究函数的单调性,得到最小值即可.
解析:
(1)当![]() 时,
时, ![]()
令![]() 0,得
0,得![]()
且![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增
上单调递增
所以![]() 在
在![]() 时取得极小值为
时取得极小值为![]() .
.
(2)由已知:![]()
![]()
![]()
![]() ,使得
,使得![]()
![]() ,即:
,即: ![]()
设![]() ,则只需要函数
,则只需要函数![]() 在
在![]() 上的最小值小于零.
上的最小值小于零.
又![]()
![]() ,
,
令![]() ,得
,得![]() (舍去)或
(舍去)或![]() .
.
①当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,
故![]() 在
在![]() 上的最小值为
上的最小值为![]() ,由
,由![]() ,可得
,可得![]() .
.
因为![]() ,所以
,所以![]() .
.
②当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,
故![]() 在
在![]() 上的最小值为
上的最小值为![]() ,由
,由![]() ,
,
可得![]() (满足
(满足![]() ).
).
③当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,故
上单调递增,故![]() 在
在![]() 上的最小值为
上的最小值为![]() .
.
因为![]() ,所以
,所以![]() ,
,
所以![]() ,即
,即![]() ,不满足题意,舍去.
,不满足题意,舍去.
综上可得![]() 或
或![]() ,
,
所以实数![]() 的取值范围为
的取值范围为![]() .
.

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案【题目】下表中的数表为“森德拉姆筛”(森德拉姆,东印度学者),其特点是每行每列都成等差数列.
2 | 3 | 4 | 5 | 6 | 7 | … |
3 | 5 | 7 | 9 | 11 | 13 | … |
4 | 7 | 10 | 13 | 16 | 19 | … |
5 | 9 | 13 | 17 | 21 | 25 | … |
6 | 11 | 16 | 21 | 26 | 31 | … |
7 | 13 | 19 | 25 | 31 | 37 | … |
… | … | … | … | … | … | … |
在上表中,2017出现的次数为( )
A. 18 B. 36 C. 48![]() D. 72
D. 72
【题目】从甲、乙两名学生中选拔一人参加射箭比赛,为此需要对他们的射箭水平进行测试.现这两名学生在相同条件下各射箭10次,命中的环数如下:
甲 | 8 | 9 | 7 | 9 | 7 | 6 | 10 | 10 | 8 | 6 |
乙 | 10 | 9 | 8 | 6 | 8 | 7 | 9 | 7 | 8 | 8 |
(1)计算甲、乙两人射箭命中环数的平均数和标准差;
(2)比较两个人的成绩,然后决定选择哪名学生参加射箭比赛.
【题目】某班同学利用国庆节进行社会实践,对![]() 岁的人群随机抽取
岁的人群随机抽取![]() 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
组数 | 分组 | 低碳族的人数 | 占本组的频率 |
第一组 |
| 120 | 0.6 |
第二组 |
| 195 |
|
第三组 |
| 100 | 0.5 |
第四组 |
|
| 0.4 |
第五组 |
| 30 | 0.3 |
第六组 |
| 15 | 0.3 |
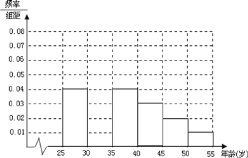
(1)补全频率分布直方图并求![]() 、
、![]() 、
、![]() 的值;
的值;
(2)从![]() 岁年龄段的“低碳族”中采用分层抽样法抽取18人参加户外低碳体验活动,如何抽取?
岁年龄段的“低碳族”中采用分层抽样法抽取18人参加户外低碳体验活动,如何抽取?