题目内容
18.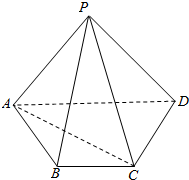 如图四棱锥P-ABCD的底面是梯形,BC∥AD,AB=BC=CD=1,AD=2,平面PAC⊥平面ABCD.
如图四棱锥P-ABCD的底面是梯形,BC∥AD,AB=BC=CD=1,AD=2,平面PAC⊥平面ABCD.(1)求证:AP⊥CD;
(2)当PA=PC=$\frac{\sqrt{6}}{2}$时,求二面角B-AP-D平面角的余弦值.
分析 (1)由已知条件推导出AC⊥DC,从而得到DC⊥平面APC,由此能证明AP⊥CD.
(2)取AC中点O,以O为原点,OB为x轴,OC为y轴,OP为z轴,建立空间直角坐标系,由此能求出二面角B-AP-D平面角的余弦值.
解答 (1)证明:∵棱锥P-ABCD的底面是梯形,BC∥AD,AB=BC=CD=1,AD=2,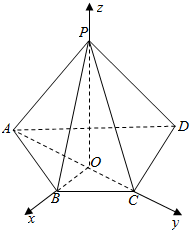
∴∠ABC=∠BCD=120°,∠BAD=∠CAD=60°,∠BAC=∠BCA=30°,
∴∠ACD=90°,即AC⊥DC,
∵平面PAC⊥平面ABCD,
∴DC⊥平面APC,
∵AP?平面APC,∴AP⊥CD.
(2)解:取AC中点O,连结PO,BO,
∵PA=PC=$\frac{\sqrt{6}}{2}$,∴PO⊥AC,
由(1)知DC⊥AC,AC=$\sqrt{3}$,∴OB⊥AC,且OB=$\frac{1}{2}DC=\frac{1}{2}$,
以O为原点,OB为x轴,OC为y轴,OP为z轴,建立空间直角坐标系,
则B($\frac{1}{2},0,0$),A(0,-$\frac{\sqrt{3}}{2}$,0),P(0,0,$\frac{\sqrt{3}}{2}$),D(-1,$\frac{\sqrt{3}}{2}$,0),
$\overrightarrow{AP}$=(0,$\frac{\sqrt{3}}{2}$,$\frac{\sqrt{3}}{2}$),$\overrightarrow{AB}$=($\frac{1}{2},\frac{\sqrt{3}}{2}$,0),$\overrightarrow{AD}$=(-1,$\sqrt{3}$,0),
设平面ABP的法向量$\overrightarrow{n}=(x,y,z)$,
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AP}=\frac{\sqrt{3}}{2}y+\frac{\sqrt{3}}{2}z=0}\\{\overrightarrow{n}•\overrightarrow{AB}=\frac{1}{2}x+\frac{\sqrt{3}}{2}y=0}\end{array}\right.$,取x=$\sqrt{3}$,得$\overrightarrow{n}$=($\sqrt{3}$,-1,1),
设平面ADP的法向量$\overrightarrow{m}=(a,b,c)$,
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{AP}=\frac{\sqrt{3}}{2}b+\frac{\sqrt{3}}{2}c=0}\\{\overrightarrow{m}•\overrightarrow{AD}=-a+\sqrt{3}b=0}\end{array}\right.$,取a=$\sqrt{3}$,得$\overrightarrow{m}$=($\sqrt{3}$,1,-1),
设二面角B-AP-D平面角为α,
cosα=|cos<$\overrightarrow{m},\overrightarrow{n}$>|=|$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}|•|\overrightarrow{n}|}$|=|$\frac{3-1-1}{\sqrt{5}•\sqrt{5}}$|=$\frac{1}{5}$.
∴二面角B-AP-D平面角的余弦值为$\frac{1}{5}$.
点评 本题考查异面直线垂直的证明,考查二面角的余弦值的求法,是中档题,解题时要注意向量法的合理运用.

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案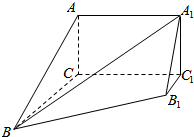 如图,几何体ABC-A1B1C1中,平面ABC∥平面A1B1C1,平面ACC1A1为矩形,平面ACC1A1⊥平面BCC1B1,已知AC=3,BC=AA1=4,BB1=5,B1C1=1
如图,几何体ABC-A1B1C1中,平面ABC∥平面A1B1C1,平面ACC1A1为矩形,平面ACC1A1⊥平面BCC1B1,已知AC=3,BC=AA1=4,BB1=5,B1C1=1