题目内容
8．等比数列中，a1=a，公比为q，前n项和Sn，求S1+S2+S3+…+Sn．分析 分别就当q=1和q≠1时，利用等差数列和等比数列的求和公式可得．
解答 解：当q=1时，an=a，前n项和Sn=na，
∴S1+S2+S3+…+Sn=（1+2+3+…+n）a=$\frac{n（n+1）}{2}$a；
当q≠1时，前n项和Sn=$\frac{a（1-{q}^{n}）}{1-q}$，
∴S1+S2+S3+…+Sn=$\frac{a}{1-q}$（n-q-q2-…-qn）
=$\frac{an}{1-q}$-$\frac{aq（1-{q}^{n}）}{（1-q）^{2}}$
点评 本题考查等比数列的求和公式，涉及分类讨论的思想，属中档题．
练习册系列答案
相关题目
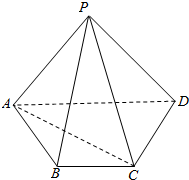如图四棱锥P-ABCD的底面是梯形，BC∥AD，AB=BC=CD=1，AD=2，平面PAC⊥平面ABCD．