题目内容
13.已知函数y=$\frac{x+1-a}{a-x}$.(1)若函数图象的对称中心是(2,-1),求a的值;
(2)若a+1≤x≤a+2,求函数值y的取值范围.
分析 (1)利用分式函数的性质,结合函数图象的对称中心是(2,-1),即可求a的值;
(2)根据分式函数的单调性进行求解即可.
解答 解:(1)y=$\frac{x+1-a}{a-x}$=$\frac{x-a}{a-x}$+$\frac{1}{a-x}$=-1-$\frac{1}{x-a}$,
则函数的对称中心为(a,-1),
∵函数图象的对称中心是(2,-1),
∴a=2;
(2)∵y=-1-$\frac{1}{x-a}$,在a+1≤x≤a+2上为增函数,
∴当x=a+1时,函数取得最小值y=-1-$\frac{1}{a+1-a}$=-1-1=-2,
当x=a+2时,函数取得最大值y=-1-$\frac{1}{a+2-a}$=-1-$\frac{1}{2}$=-$\frac{3}{2}$,
即-2≤y≤-$\frac{3}{2}$.
点评 本题主要考查分式函数的对称性以及函数最值的求解,利用分子常数化是解决本题的关键.

练习册系列答案
相关题目
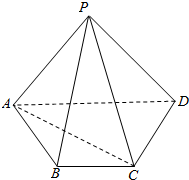 如图四棱锥P-ABCD的底面是梯形,BC∥AD,AB=BC=CD=1,AD=2,平面PAC⊥平面ABCD.
如图四棱锥P-ABCD的底面是梯形,BC∥AD,AB=BC=CD=1,AD=2,平面PAC⊥平面ABCD.