题目内容
11.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+y2=1(a>1)的右焦点为F(1,0),过点F且不与坐标轴垂直的直线x=my+1交椭圆C于A,B两点,线段AB的垂直平分线与x轴交于点G(t,0).(Ⅰ)当t=0时,求实数m的值;
(Ⅱ)求证:对于任意的实数m,都不存在直线AB,使得AG⊥BG.
分析 (Ⅰ)当t=0时,线段AB的垂直平分线过原点,可得kOD=-$\frac{1}{m}$,即可求实数m的值;
(Ⅱ)求出G的坐标,证明$\overrightarrow{AG}$•$\overrightarrow{BG}$<0,即可证明对于任意的实数m,都不存在直线AB,使得AG⊥BG.
解答 (Ⅰ)解:∵椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+y2=1(a>1)的右焦点为F(1,0),
∴a=2,
∴椭圆的方程为$\frac{{x}^{2}}{2}$+y2=1
设直线AB的方程为x=my+1,
与椭圆方程联立可得可得(m2+2)y2+2my-1=0.
记A(x1,y1),B(x2,y2),AB中点N(x0,y0),
则y1+y2=$\frac{-2m}{{m}^{2}+2}$,y1y2=-$\frac{1}{{m}^{2}+2}$.
可得y0=$\frac{-m}{{m}^{2}+2}$,x0=mx0+1=$\frac{2}{{m}^{2}+2}$
∵t=0,
∴线段AB的垂直平分线过原点,
∴kOD=-$\frac{1}{m}$,
∴-$\frac{m}{2}$=-$\frac{1}{m}$,
∴m=±$\sqrt{2}$;
(Ⅱ)证明:线段AB的垂直平分线的方程为y-$\frac{-m}{{m}^{2}+2}$=-$\frac{1}{m}$(x-$\frac{2}{{m}^{2}+2}$),
令y=0,可得x=$\frac{2-{m}^{2}}{{m}^{2}+2}$,即t=$\frac{2-{m}^{2}}{{m}^{2}+2}$,
∴$\overrightarrow{AG}$•$\overrightarrow{BG}$=A(t-x1,-y1)•(t-x2,-y2)=t2-t(x1+x2)+x1x2+y1y2=$\frac{-({m}^{2}+\frac{3}{2})^{2}-\frac{1}{4}}{({m}^{2}+2)^{2}}$<0,
∴对于任意的实数m,都不存在直线AB,使得AG⊥BG.
点评 本题考查椭圆的方程,考查直线与椭圆的位置关系,考查向量知识的运用,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案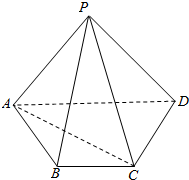 如图四棱锥P-ABCD的底面是梯形,BC∥AD,AB=BC=CD=1,AD=2,平面PAC⊥平面ABCD.
如图四棱锥P-ABCD的底面是梯形,BC∥AD,AB=BC=CD=1,AD=2,平面PAC⊥平面ABCD.