题目内容
4.已知直线l:$\left\{\begin{array}{l}{x=-1+tcosα}\\{y=tsinα}\end{array}\right.$(t为参数,α为l的倾斜角,且0<α<π)与曲线C:$\left\{\begin{array}{l}{x=\sqrt{2}cosθ}\\{y=sinθ}\end{array}\right.$(θ为参数)相交于A、B两点,点F的坐标为(1,0).(1)求△ABF的周长;
(2)若点E(-1,0)恰为线段AB的三等分点,求△ABF的面积.
分析 (1)运用同角的平方关系和代入法,化参数方程为普通方程,再由椭圆的定义,即可得到所求三角形ABF的周长;
(2)联立直线方程和椭圆方程,消去x,运用韦达定理和三等分点,求得|y1-y2|,进而运用三角形的面积公式,计算即可得到.
解答 解:(1)曲线C:$\left\{\begin{array}{l}{x=\sqrt{2}cosθ}\\{y=sinθ}\end{array}\right.$化为普通方程为$\frac{{x}^{2}}{2}$+y2=1,
直线L:$\left\{\begin{array}{l}{x=-1+tcosα}\\{y=tsinα}\end{array}\right.$化为普通方程为y=tanα•(x+1),
直线恒过椭圆的左焦点F'(-1,0),
由椭圆的定义可得,△ABF的周长为|AF'|+|AF|+|BF'|+|BF|=4a=4$\sqrt{2}$;
(2)设A(x1,y1),B(x2,y2),
将直线方程代入椭圆方程,消去x,可得(2+cot2α)y2-2cotα•y-1=0,
则y1+y2=$\frac{2cotα}{2+co{t}^{2}α}$,y1y2=-$\frac{1}{2+co{t}^{2}α}$,①
点E(-1,0)恰为线段AB的三等分点,即有2y1=-y2,②
解得cotα=±$\frac{\sqrt{14}}{7}$,
则△ABF的面积为S=$\frac{1}{2}$|FF'|•|y1-y2|=|y1-y2|=$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$=$\frac{3\sqrt{14}}{8}$.
点评 本题主要考查参数方程和普通方程的互化,同时考查椭圆的定义和直线和椭圆方程联立,运用韦达定理和弦长公式,考查运算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案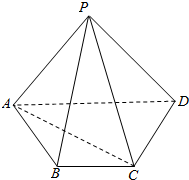 如图四棱锥P-ABCD的底面是梯形,BC∥AD,AB=BC=CD=1,AD=2,平面PAC⊥平面ABCD.
如图四棱锥P-ABCD的底面是梯形,BC∥AD,AB=BC=CD=1,AD=2,平面PAC⊥平面ABCD.