题目内容
【题目】已知不共线向量![]() ,
,![]() 满足|
满足|![]() |=3,|
|=3,|![]() |=2,(2
|=2,(2![]() 3
3![]() )(2
)(2![]() )=20.
)=20.
(1)求![]()
![]() ;
;
(2)是否存在实数λ,使λ![]() 与
与![]() 2
2![]() 共线?
共线?
(3)若(k![]() 2
2![]() )⊥(
)⊥(![]() ),求实数k的值.
),求实数k的值.
【答案】(1)1;(2)存在,![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)利用向量运算法则展开计算得到答案.
(2)假设存在实数λ,使λ![]() 与
与![]() 2
2![]() 共线,则
共线,则![]() ,计算得到答案.
,计算得到答案.
(3)计算(k![]() 2
2![]() )(
)(![]() )=0,展开计算得到答案.
)=0,展开计算得到答案.
(1)向量![]() ,
,![]() 满足|
满足|![]() |=3,|
|=3,|![]() |=2,(2
|=2,(2![]() 3
3![]() )(2
)(2![]() )=20,
)=20,
所以4![]() 4
4![]()
![]() 3
3![]() 4×9﹣4
4×9﹣4![]()
![]() 3×4=20,解得
3×4=20,解得![]()
![]() 1;
1;
(2)假设存在实数λ,使λ![]() 与
与![]() 2
2![]() 共线,则
共线,则![]() ,
,
故![]() ,
,![]() .
.
即存在λ![]() ,使得λ
,使得λ![]() 与
与![]() 2
2![]() 共线;
共线;
(3)若(k![]() 2
2![]() )⊥(
)⊥(![]() ),则(k
),则(k![]() 2
2![]() )(
)(![]() )=0,
)=0,
即k![]() (2﹣k2)
(2﹣k2)![]()
![]() 2k
2k![]() 0,所以9k+(2﹣k2)×1﹣2k4=0,
0,所以9k+(2﹣k2)×1﹣2k4=0,
整理得k2﹣k﹣2=0,解得k=﹣1或k=2.

练习册系列答案
相关题目
【题目】某市电视台为了宣传举办问答活动,随机对该市15~65岁的人群抽样了![]() 人,回答问题统计结果如图表所示.
人,回答问题统计结果如图表所示.
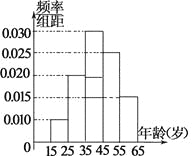
组号 | 分组 | 回答正确 | 回答正确的人数 |
第1组 |
| 5 | 0.5 |
第2组 |
|
| 0.9 |
第3组 |
| 27 |
|
第4组 |
|
| 0.36 |
第5组 |
| 3 |
|
(Ⅰ) 分别求出![]() 的值;
的值;
(Ⅱ) 从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,则第2,3,4组每组应各抽取多少人?
(Ⅲ) 在(Ⅱ)的前提下,电视台决定在所抽取的6人中随机抽取2人颁发幸运奖,求:所抽取的人中第2组至少有1人获得幸运奖的概率.