题目内容
【题目】上周某校高三年级学生参加了数学测试，年级组织任课教师对这次考试进行成绩分析现从中随机选取了40名学生的成绩作为样本，已知这40名学生的成绩全部在40分至100分之间，现将成绩按如下方式分成6组：第一组；第二组；……；第六组，并据此绘制了如图所示的频率分布直方图．
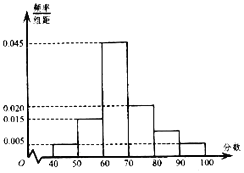
（1）估计这次月考数学成绩的平均分和众数；
（2）从成绩大于等于80分的学生中随机选2名，求至少有1名学生的成绩在区间
内的概率．
【答案】（1）平均分68，众数65；（2）
【解析】
（1）先求得成绩在区间
内的频率，然后根据平均数的计算公式，计算出平均分，利用最高的小长方形求得众数.
（2）先求得、
的人数，然后用列举法，结合古典概型概率计算公式，计算出所求概率.
（1）因各组的频率之和为1，所以成绩在区间内的频率为
.
所以平均分
，
众数的估计值是65.
（2）设
表示事件“在成绩大于等于80分的学生中随机选2名，至少有1名学生的成绩在区间内”，
由题意可知成绩在区间内的学生所选取的有：
人，
记这4名学生分别为
，
，
，
，
成绩在区间内的学生有
人，记这2名学生分别为
，
，
则从这6人中任选2人的基本事件为：
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，共15种，
事件“至少有1名学生的成绩在区间内”的可能结果为：，，，，
，，，，，共9种，所以
．
故所求事件的概率为：．
名校联盟快乐课堂系列答案
【题目】某市A，B，C，D四所中学报名参加某高校2015年自主招生考试的学生人数如下表所示：
中学 | A | B | C | D |
人数 | 40 | 30 | 10 | 20 |
该市教委为了解参加考试的学生的学习状况，采用分层抽样的方法从四所中学报名参加考试的学生中随机抽取50名参加问卷调查.则A，B，C，D四所中学抽取的学生人数分别为（ ）
A.15，20，10，5B.15，20，5，10
C.20，15，10，5D.20，15，5，10
