题目内容
【题目】已知实数![]() ,设函数
,设函数![]()
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)对任意![]() 均有
均有![]() 求
求![]() 的取值范围.
的取值范围.
注:![]() 为自然对数的底数.
为自然对数的底数.
【答案】(1)![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() ;(2)
;(2)![]() .
.
【解析】
(1)首先求得导函数的解析式,然后结合函数的解析式确定函数的单调区间即可.
(2)由题意首先由函数在特殊点的函数值得到a的取值范围,然后证明所得的范围满足题意即可.
(1)当![]() 时,
时,![]() ,函数的定义域为
,函数的定义域为![]() ,且:
,且:
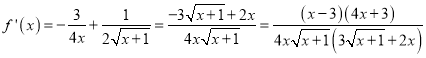 ,
,
因此函数![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() .
.
(2)构造函数![]() ,
,
注意到:![]() ,
,
注意到![]() 时
时![]() 恒成立,满足
恒成立,满足![]() ;
;
当![]() 时,
时,![]() ,不合题意,
,不合题意,
且![]() ,解得:
,解得:![]() ,故
,故![]() .
.
下面证明![]() 刚好是满足题意的实数a的取值范围.
刚好是满足题意的实数a的取值范围.
分类讨论:
(a)当![]() 时,
时,![]() ,
,
令![]() ,则:
,则:
![]()
![]()

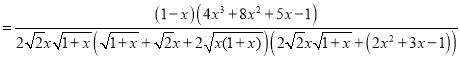 ,
,
易知![]() ,则函数
,则函数![]() 单调递减,
单调递减,![]() ,满足题意.
,满足题意.
(b)当![]() 时,
时,![]() 等价于
等价于![]() ,
,
左侧是关于a的开口向下的二次函数![]() ,
,
其判别式![]() ,
,
令![]() ,注意到当
,注意到当![]() 时,
时,![]() ,
,
于是![]() 在
在![]() 上单调递增,而
上单调递增,而![]() ,
,
于是当![]() 时命题成立,
时命题成立,
而当![]() 时,此时
时,此时![]() 的对称轴为
的对称轴为![]() 随着
随着![]() 递增,
递增,
于是对称轴在![]() 的右侧,而
的右侧,而![]() 成立,(不等式等价于
成立,(不等式等价于![]() ).
).
因此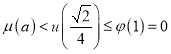 .
.
综上可得:实数a的取值范围是![]() .
.

练习册系列答案
相关题目