题目内容
8.在矩形ABCD中,AB=5,AC=7,现向该矩形ABCD内随机投一点P,则∠APB>90°的概率为$\frac{5\sqrt{6}π}{96}$.分析 由已知求出矩形的面积,以及使∠APB>90°成立的P的对应的区域面积,利用几何概型求值.
解答 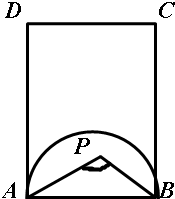 解:由题意,AD=$\sqrt{A{C}^{2}-A{B}^{2}}=2\sqrt{6}$,矩形的面积为10$\sqrt{6}$,如图
解:由题意,AD=$\sqrt{A{C}^{2}-A{B}^{2}}=2\sqrt{6}$,矩形的面积为10$\sqrt{6}$,如图
而使∠APB>90°成立的区域为以AB为直径的半圆,面积为$\frac{1}{2}π(\frac{5}{2})^{2}=\frac{25π}{8}$,
由几何概型公式得到向该矩形ABCD内随机投一点P,则∠APB>90°的概率为:$\frac{\frac{25π}{8}}{10\sqrt{6}}=\frac{5\sqrt{6}π}{96}$;
故答案为:$\frac{5\sqrt{6}π}{96}$.
点评 本题考查了几何概型的概率求法;关键是求出满足向该矩形ABCD内随机投一点P,则∠APB>90°的区域面积,利用公式解答.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
16.将正奇数1,3,5,7,…按如表的方式进行排列,记aij表示第i行第j列的数,若aij=2015,则i+j的值为( )
| 第1列 | 第2列 | 第3列 | 第4列 | 第5列 | |
| 第1行 | 1 | 3 | 5 | 7 | |
| 第2行 | 15 | 13 | 11 | 9 | |
| 第3行 | 17 | 19 | 21 | 23 | |
| 第4行 | 31 | 29 | 27 | 25 | |
| 第5行 | 39 | 37 | 35 | 33 | |
| … | … | … | … | … | … |
| A. | 505 | B. | 506 | C. | 254 | D. | 253 |
13.已知x∈R+,则x+$\frac{4}{{x}^{2}}$的最小值是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
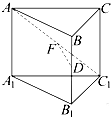 在棱长均相等的正三棱柱ABC-A1B1C1中,D为BB1的中点,F在AC1上,且DF⊥AC1,则下述结论:①AC1⊥BC;②AF=FC1;③平面DAC1⊥平面ACC1A1,其中正确的个数为( )
在棱长均相等的正三棱柱ABC-A1B1C1中,D为BB1的中点,F在AC1上,且DF⊥AC1,则下述结论:①AC1⊥BC;②AF=FC1;③平面DAC1⊥平面ACC1A1,其中正确的个数为( )