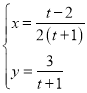题目内容
【题目】设椭圆C的方程为![]() ,O为坐标原点,A为椭团的上顶点,
,O为坐标原点,A为椭团的上顶点,![]() 为其右焦点,D是线段
为其右焦点,D是线段![]() 的中点,且
的中点,且![]() .
.
(1)求椭圆C的方程;
(2)过坐标原点且斜率为正数的直线交椭圆C于P,Q两点,分别作![]() 轴,
轴,![]() 轴,垂足分别为E,F,连接
轴,垂足分别为E,F,连接![]() ,
,![]() 并延长交椭圆C于点M,N两点.
并延长交椭圆C于点M,N两点.
(ⅰ)判断![]() 的形状;
的形状;
(ⅱ)求四边形![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() (2)(ⅰ)
(2)(ⅰ)![]() 为直角三角形(ⅱ)
为直角三角形(ⅱ)![]()
【解析】
(1)根据题意得到![]() ,在求出
,在求出![]() ,得到椭圆标准方程;(2)(ⅰ)先设直线
,得到椭圆标准方程;(2)(ⅰ)先设直线![]() 和
和![]() 的方程,分别与椭圆方程联立,得到点
的方程,分别与椭圆方程联立,得到点![]() 的坐标,从而表示出直线
的坐标,从而表示出直线![]() 的斜率,得到
的斜率,得到![]() ,从而做出判断;(ⅱ)先得到四边形
,从而做出判断;(ⅱ)先得到四边形![]() 面积是
面积是![]() 面积的2倍,利用弦长公式得到
面积的2倍,利用弦长公式得到![]() ,
,![]() ,从而表示出
,从而表示出![]() 的面积,再利用基本不等式得到其最大值,从而得到四边形
的面积,再利用基本不等式得到其最大值,从而得到四边形![]() 面积的最大值.
面积的最大值.
解:(1)设椭圆的半焦距为c.
由题意可得![]() ,D为
,D为![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴椭圆的方程为![]() .
.
(2)(1)设直线![]() 的方程为
的方程为![]() ,且点P在第一象限,
,且点P在第一象限,
联立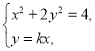 消去y得
消去y得![]() ,
,
显然![]() ,
,
∴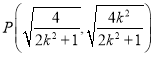 ,
,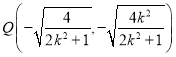 .
.
又∵![]() 轴,∴
轴,∴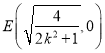 ,
,
∴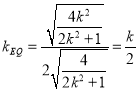 ,
,
∴直线![]() 的方程为
的方程为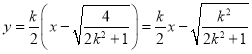 ,
,
联立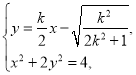 消去y得
消去y得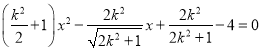 ,
,
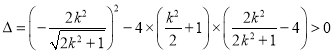 ,
,
∴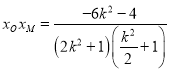 .
.
∵![]() ,
,
∴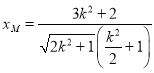 ,
,
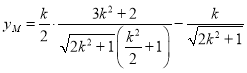 ,
,
∴![]() ,
,
∴![]() ,
,
即![]() 为直角三角形.
为直角三角形.
(ⅱ)根据图形的对称性可知,四边形![]() 面积是
面积是![]() 面积的2倍,
面积的2倍,
由(ⅰ)知![]() 为直角三角形,且
为直角三角形,且![]() ,
,
∴![]() .
.
又![]()
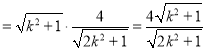 ,
,
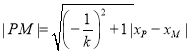
 ,
,
∴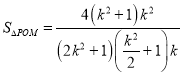

![]()
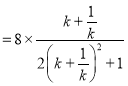 .
.
令![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
∴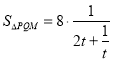 ,而
,而![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,所以
,所以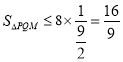
即当![]() 时,
时,![]() 最大,此时
最大,此时![]() 的面积也达到最大,
的面积也达到最大,
由对称性可知![]() ,
,
故当![]() 时,
时,![]() 最大,
最大,
![]() .
.

 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案【题目】“初中数学靠练,高中数学靠悟”.总结反思自己已经成为数学学习中不可或缺的一部分,为了了解总结反思对学生数学成绩的影响,某校随机抽取200名学生,抽到不善于总结反思的学生概率是0.6.
(1)完成![]() 列联表(应适当写出计算过程);
列联表(应适当写出计算过程);
(2)试运用独立性检验的思想方法分析是否有![]() 的把握认为学生的学习成绩与善于总结反思有关.
的把握认为学生的学习成绩与善于总结反思有关.
统计数据如下表所示:
不善于总结反思 | 善于总结反思 | 合计 | |
学习成绩优秀 | 40 | ||
学习成绩一般 | 20 | ||
合计 | 200 |
参考公式:![]() 其中
其中![]()