题目内容
【题目】曲线![]() 的极坐标方程为
的极坐标方程为![]() (常数
(常数![]() ),曲线
),曲线![]() 的参数方程为
的参数方程为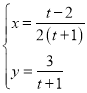 (
(![]() 为参数).
为参数).
(1)求曲线![]() 的直角坐标方程和
的直角坐标方程和![]() 的普通方程;
的普通方程;
(2)若曲线![]() ,
,![]() 有两个不同的公共点,求实数
有两个不同的公共点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() :
:![]() ,
,![]() :
:![]() ;(2)
;(2)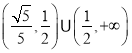
【解析】
(1)根据直角坐标与极坐标关系及题目条件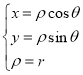 得曲线
得曲线![]() 的直角坐标方程,利用消元法消去t可得
的直角坐标方程,利用消元法消去t可得![]() 的普通方程;
的普通方程;
(2)若曲线![]() ,
,![]() 有两个不同的公共点,法一:方程联立利用根与系数关系,利用判别式解出即可求实数
有两个不同的公共点,法一:方程联立利用根与系数关系,利用判别式解出即可求实数![]() 的取值范围;法二:数形结合可得圆心到直线距离小于半径,解出即可求实数
的取值范围;法二:数形结合可得圆心到直线距离小于半径,解出即可求实数![]() 的取值范围.
的取值范围.
(1)方法一:由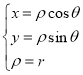 得:
得:![]() .
.
由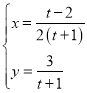 得:
得:![]() ,即
,即![]() .
.
∴曲线![]() 的直角坐标方程为:
的直角坐标方程为:![]() ,
,![]() 的普通方程为:
的普通方程为:![]() .
.
方法二:由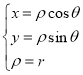 得:
得:![]() .
.
由![]() 得:
得:![]() ;由
;由![]() 得:
得:![]() .
.
∴![]() .
.
整理得![]() 的普通方程为:
的普通方程为:![]() .
.
∴曲线![]() 的直角坐标方程为:
的直角坐标方程为:![]() ,
,![]() 的普通方程为:
的普通方程为:![]() .
.
(2)方法一:由![]() 消
消![]() 得:
得:![]() .
.
由曲线![]() ,
,![]() 有两个不同的公共点得:
有两个不同的公共点得:![]() ,
,![]() 解得:
解得:![]() .
.
又当圆![]() :
:![]() 过点
过点![]() 时,有
时,有![]() ,且曲线
,且曲线![]() 表示不过点
表示不过点![]() 的直线.
的直线.
∴![]() .
.
∴实数![]() 的取值范围为
的取值范围为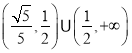 .
.
方法二:圆心![]() 到直线
到直线![]() 的距离为:
的距离为:![]() .
.
由曲线![]() ,
,![]() 有两个不同的公共点得:
有两个不同的公共点得:![]() ,即
,即![]() .
.
又当圆![]() :
:![]() 过点
过点![]() 时,有
时,有![]() ,且曲线
,且曲线![]() 表示不过点
表示不过点![]() 的直线.
的直线.
∴![]() .
.
∴实数![]() 的取值范围为
的取值范围为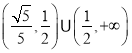 .
.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案【题目】第十三届全国人大常委会第十一次会议审议的《固体废物污染环境防治法(修订草案)》中,提出推行生活垃圾分类制度,这是生活垃圾分类首次被纳入国家立法中.为了解某城市居民的垃圾分类意识与政府相关法规宣传普及的关系,对某试点社区抽取![]() 户居民进行调查,得到如下的
户居民进行调查,得到如下的![]() 列联表.
列联表.
分类意识强 | 分类意识弱 | 合计 | |
试点后 |
| ||
试点前 |
| ||
合计 |
|
已知在抽取的![]() 户居民中随机抽取
户居民中随机抽取![]() 户,抽到分类意识强的概率为
户,抽到分类意识强的概率为![]() .
.
(1)请将上面的![]() 列联表补充完整,并判断是否有
列联表补充完整,并判断是否有![]() 的把握认为居民分类意识的强弱与政府宣传普及工作有关?说明你的理由;
的把握认为居民分类意识的强弱与政府宣传普及工作有关?说明你的理由;
(2)已知在试点前分类意识强的![]() 户居民中,有
户居民中,有![]() 户自觉垃圾分类在
户自觉垃圾分类在![]() 年以上,现在从试点前分类意识强的
年以上,现在从试点前分类意识强的![]() 户居民中,随机选出
户居民中,随机选出![]() 户进行自觉垃圾分类年限的调查,记选出自觉垃圾分类年限在
户进行自觉垃圾分类年限的调查,记选出自觉垃圾分类年限在![]() 年以上的户数为
年以上的户数为![]() ,求
,求![]() 分布列及数学期望.
分布列及数学期望.
参考公式: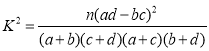 ,其中
,其中![]() .
.
下面的临界值表仅供参考
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
