题目内容
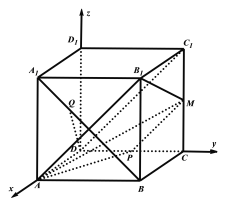
【题目】如图，在棱长为1的正方体
中，
分别为棱
的中点.
为面对角线
上任一点，则下列说法正确的是（ ）
A.平面
内存在直线与
平行
B.平面截正方体所得截面面积为
C.直线
和
所成角可能为60°
D.直线和所成角可能为30°
【答案】BC
【解析】
，直线
相交，得到
与平面
位置关系，即可判断选项A真假；
，而
，得到
，可得截面为等腰梯形
，求出面积即可判断选项B；建立空间直角坐标系，求出直线
和
所成角余弦值的范围，即可判断选项C，D.
对于选项A，在正方体
中，，
在平面
中，直线相交，所以直线
与平面相交，
故直线与平面相交，则平面不存在直线与平行，
所以选项A错误；
对于选项B，连接
分别为棱
的中点，
所以
，在正方体中，
，所以
，连
，则梯形为所求的截面，
，所以等腰梯形的高为
，
所以梯形的面积为
，选项B正确；
对于选项C,D，以
为坐标原点，
所在的直线分别为
轴，
建立空间直角坐标系，
，
设
，
，
，
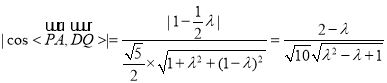
，令
，
，
，
，而
，
直线和所成角可能为60°，但不可能为30°，
选项C正确，选项D错误.
故选：BC.
练习册系列答案
相关题目
