Ő‚ńŅńŕ»›
°ĺŐ‚ńŅ°Ņ2022ńÍĪĪĺ©∂¨ľĺį¬‘ňĽŠľīĶŕ24Ĺž∂¨ľĺį¬Ń÷∆•Ņň‘ň∂ĮĽŠ£¨Ĺę‘ŕ2022ńÍ2‘¬4÷Ń2‘¬20»’‘ŕĪĪĺ©ļÕ’Ňľ“ŅŕŃ™ļŌĺŔ––.ń≥—–ĺŅĽķĻĻő™ŃňĹ‚īů—ß…ķ∂‘ĪýļÝ‘ň∂ĮĶń–ň»§£¨ňśĽķī”ń≥īů—ß—ß…ķ÷–≥ť»°Ńň120»ňĹÝ––Ķų≤ť£¨ĺ≠Õ≥ľ∆ń–…ķ”ŽŇģ…ķĶń»ň ż÷ģĪ»ő™11£ļ13£¨ń–…ķ÷–”–30»ňĪŪ ĺ∂‘ĪýļÝ‘ň∂Į”––ň»§£¨Ňģ…ķ÷–”–15»ňĪŪ ĺ∂‘ĪýļÝ‘ň∂Į√Ľ”––ň»§.
£®1£©ÕÍ≥…2°Ń2Ń–Ń™ĪŪ£¨≤ĘĽōīūń‹∑Ů”–99%Ķńį—ő’»Ōő™°į∂‘ĪýļÝ «∑Ů”––ň»§”Ž–‘Īū”–Ļō°Ī£Ņ
”––ň»§ | √Ľ”––ň»§ | ļŌľ∆ | |
ń– | 30 | ||
Ňģ | 15 | ||
ļŌľ∆ | 120 |
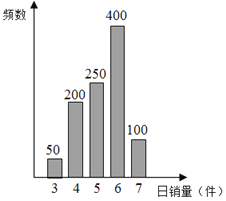
£®2£©»ŰĹę∆Ķ¬ ”ő™łŇ¬ £¨Ō÷‘Ŕī”ł√–£»ęŐŚ—ß…ķ÷–£¨≤…”√ňśĽķ≥ť—ýĶń∑Ĺ∑®√Ņīő≥ť»°1√Ż—ß…ķ£¨≥ť»°5īő£¨ľ«ĪĽ≥ť»°Ķń5√Ż—ß…ķ÷–∂‘ĪýļÝ”––ň»§Ķń»ň żő™X£¨»Ű√Ņīő≥ť»°ĶńĹŠĻŻ «ŌŗĽ•∂ņŃĘĶń£¨«ůXĶń∑÷≤ľŃ–£¨∆ŕÕŻļÕ∑Ĺ≤Ó.
łĹ£ļ≤őŅľĻę Ĺ![]() £¨∆š÷–n£Ĺa+b+c+d.
£¨∆š÷–n£Ĺa+b+c+d.
ŃŔĹÁ÷ĶĪŪ£ļ
P£®K2°›K0£© | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
K0 | 2.072 | 2.076 | 3.841 | 5.024 | 6.635 |
°ĺīūįł°Ņ£®1£©ŐÓĪŪľŻĹ‚őŲ£Ľ”–99%Ķńį—ő’»Ōő™°į∂‘ĪýļÝ «∑Ů”––ň»§”Ž–‘Īū”–Ļō°Ī£®2£©ŌÍľŻĹ‚őŲ
°ĺĹ‚őŲ°Ņ
£®1£©Ō»łýĺ›Ī»ņżĻōŌĶ«ůĹ‚ń–ŇģÕ¨—ßĶń»ň ż£¨ÕÍ≥…ĪŪłŮ£¨«ůĹ‚ĻŘ≤‚÷ĶĶ√≥ŲĹŠ¬Ř£Ľ
£®2£©łýĺ›∂ĢŌÓ∑÷≤ľĶńŐōĶ„«ůĹ‚∑÷≤ľŃ–ļÕ∆ŕÕŻ°Ę∑Ĺ≤Ó.
£®1£©“Úő™ń–…ķ”ŽŇģ…ķĶń»ň ż÷ģĪ»ő™11£ļ13£¨«“◊‹»ň żő™120£¨ňý“‘ń–…ķĻ≤”–55»ň£¨Ňģ…ķĻ≤”–65»ň£ĽĪŪłŮ»ÁŌ¬£ļ
”––ň»§ | √Ľ”––ň»§ | ļŌľ∆ | |
ń– | 30 | 25 | 55 |
Ňģ | 50 | 15 | 65 |
ļŌľ∆ | 80 | 40 | 120 |
łýĺ›ĪŪłŮ«ů≥ŲK2![]() £¨
£¨
Ļ ”–99%Ķńį—ő’»Ōő™°į∂‘ĪýļÝ «∑Ů”––ň»§”Ž–‘Īū”–Ļō°Ī.
£®2£©”…Ń–ĪŪŅ…÷™£¨∂‘ĪýļÝ”––ň»§Ķń—ß…ķ∆Ķ¬ ő™![]() £¨Ĺę∆š ”ő™łŇ¬ £¨
£¨Ĺę∆š ”ő™łŇ¬ £¨
”…Ő‚“‚X°ęB£®5£¨![]() £©£¨
£©£¨
X | 0 | 1 | 2 | 3 | 4 | 5 |
P |
|
|
|
|
|
|
E£®X£©£Ĺnp![]() £¨D£®x£©£Ĺnpq
£¨D£®x£©£Ĺnpq![]() .
.

 √ŻŐ‚—ĶŃ∑ŌĶŃ–īūįł
√ŻŐ‚—ĶŃ∑ŌĶŃ–īūįł ∆ŕń©ľĮĹŠļŇŌĶŃ–īūįł
∆ŕń©ľĮĹŠļŇŌĶŃ–īūįł