题目内容
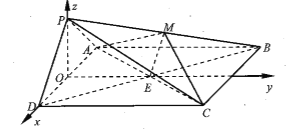
【题目】如图,在四棱锥P-ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点M在线段PPD//平面MAC,PA=PD=![]() ,AB=4.
,AB=4.
(I)求证:M为PB的中点;
(II)求二面角B-PD-A的大小;
(III)求直线MC与平面BDP所成角的正弦值.

【答案】(1)见解析(2)![]() (3)
(3)![]()
【解析】试题分析:(Ⅰ)设![]() 交点为
交点为![]() ,连接
,连接![]() ,因为线面平行,即
,因为线面平行,即![]() 平面
平面![]() ,根据性质定理,可知线线平行,即
,根据性质定理,可知线线平行,即![]() ,再由
,再由![]() 为
为![]() 的中点,可知
的中点,可知![]() 为
为![]() 的中点;(Ⅱ)因为平面
的中点;(Ⅱ)因为平面![]() 平面
平面![]() ,
, ![]() ,所以取
,所以取![]() 的中点
的中点![]() 为原点建立空间直角坐标系,根据向量法先求两平面的法向量
为原点建立空间直角坐标系,根据向量法先求两平面的法向量![]() ,
, ![]() ,再根据公式
,再根据公式![]() ,求二面角的大小;(Ⅲ)根据(Ⅱ)的结论,直接求
,求二面角的大小;(Ⅲ)根据(Ⅱ)的结论,直接求![]() 即可.
即可.
试题解析:解:(I)设![]() 交点为
交点为![]() ,连接
,连接![]() .
.
因为![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() 是正方形,所以
是正方形,所以![]() 为
为![]() 的中点,所以
的中点,所以![]() 为
为![]() 的中点.
的中点.
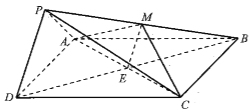
(II)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
, ![]() .
.
因为![]() ,所以
,所以![]() .
.
又因为平面![]() 平面
平面![]() ,且
,且![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() 是正方形,所以
是正方形,所以![]() .
.
如图建立空间直角坐标系![]() ,则
,则![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则![]() ,即
,即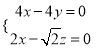 .
.
令![]() ,则
,则![]() ,
, ![]() .于是
.于是![]() .
.
平面![]() 的法向量为
的法向量为![]() ,所以
,所以![]() .
.
由题知二面角![]() 为锐角,所以它的大小为
为锐角,所以它的大小为![]() .
.
(III)由题意知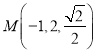 ,
, ![]() ,
, 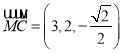 .
.
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则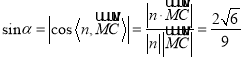 .
.
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

练习册系列答案
相关题目
【题目】某批次的某种灯泡![]() 个,对其寿命进行追踪调查,将结果列成频率分布表如下,根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于
个,对其寿命进行追踪调查,将结果列成频率分布表如下,根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于![]() 天的灯泡是优等品,寿命小于
天的灯泡是优等品,寿命小于![]() 天的灯泡是次品,其余的灯泡是正品.
天的灯泡是次品,其余的灯泡是正品.
寿命 (天) | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
(1)根据频率分布表中的数据,写出![]() 的值;
的值;
(2)某人从这![]() 个灯泡中随机地购买了
个灯泡中随机地购买了![]() 个,求此灯泡恰好不是次品的概率;
个,求此灯泡恰好不是次品的概率;
(3)某人从这批灯泡中随机地购买了![]() 个,如果这
个,如果这![]() 个灯泡的等级情況恰好与按三个等级分层抽样所得的结果相同,求
个灯泡的等级情況恰好与按三个等级分层抽样所得的结果相同,求![]() 的最小值.
的最小值.