题目内容
【题目】已知函数f(x)=|2x+3|+|2x﹣1|.
(1)求不等式f(x)≤6的解集;
(2)若关于x的不等式f(x)<|m﹣1|的解集非空,求实数m的取值范围.
【答案】(1){x|﹣2≤x≤1};(2)m<﹣3或m>5.
【解析】
(1)把![]() 作为一个数和,利用绝对值的几何意义解不等式;
作为一个数和,利用绝对值的几何意义解不等式;
(2)问题可化为![]() ,同样利用绝对值的几何意义求出函数最小值,再解绝对值不等式可得.
,同样利用绝对值的几何意义求出函数最小值,再解绝对值不等式可得.
(1)不等式f(x)≤6,即|2x+3|+|2x﹣1|≤6.
不等式的几何意义,是数轴是的点2x,到﹣3与1的距离之和不大于6,
∴﹣4≤2x≤2,解得﹣2≤x≤1,
不等式的解集为{x|﹣2≤x≤1};
(2)函数f(x)=|2x+3|+|2x﹣1|.
由绝对值的几何意义可知:f(x)min=4,
关于x的不等式f(x)![]() |m﹣1|的解集非空,
|m﹣1|的解集非空,
只须:4![]() |m﹣1|,解得m
|m﹣1|,解得m![]() ﹣3或m
﹣3或m![]() 5.
5.
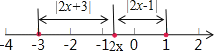

练习册系列答案
相关题目
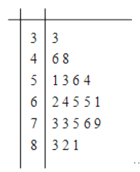
【题目】某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得到图所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意,
(1)根据以上资料完成下面的![]() 列联表,若据此数据算得
列联表,若据此数据算得![]() ,则在犯错的概率不超过
,则在犯错的概率不超过![]() 的前提下,你是否认为“满意与否”与“性别”有关?
的前提下,你是否认为“满意与否”与“性别”有关?
不满意 | 满意 | 合计 | |
男 | 4 | 7 | |
女 | |||
合计 |
附:
| 0.100 | 0.050 | 0.010 |
| 2.706 | 3.841 | 6.635 |
(2)估计用户对该公司的产品“满意”的概率;
(3)该公司为对客户做进一步的调查,从上述对其产品满意的用户中再随机选取2人,求这两人都是男用户或都是女用户的概率.


