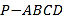题目内容
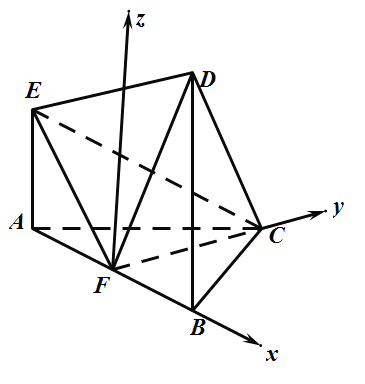
【题目】如图所示的多面体中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,且
,且![]() ,点
,点![]() 是
是![]() 的中点.
的中点.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析 (2)![]() .
.
【解析】
(1)推导出![]() ,从而
,从而![]() 平面
平面![]() ,
,![]() ,推导出
,推导出![]() ,由此能证明
,由此能证明![]() 平面
平面![]() ,从而平面
,从而平面![]() 平面
平面![]() .
.
(2)以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,过
轴,过![]() 作平面
作平面![]() 的垂线为
的垂线为![]() 轴,建立空间直角坐标系,利用向量法能求出二面角
轴,建立空间直角坐标系,利用向量法能求出二面角![]() 的余弦值.
的余弦值.
(1)证明:∵![]() ,点
,点![]() 是
是![]() 的中点,∴
的中点,∴![]() ,
,
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∵![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∵![]() 中,
中, ![]() ,∴
,∴![]() ,
,
∵![]() 中,
中, ![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
(2)解:以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,过
轴,过![]() 作平面
作平面![]() 的垂线为
的垂线为![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,
则![]() ,
, ![]() ,
,![]() ,
, ![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,
则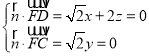 ,取
,取![]() ,得
,得![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,
则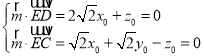 ,取
,取![]() ,得
,得![]() ,
,
设二面角![]() 的平面角为
的平面角为![]() ,
,
则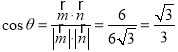 ,
,
又因为此二面角![]() 为锐二面角,
为锐二面角,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】2022年北京冬季奥运会即第24届冬季奥林匹克运动会,将在2022年2月4至2月20日在北京和张家口联合举行.某研究机构为了解大学生对冰壶运动的兴趣,随机从某大学学生中抽取了120人进行调查,经统计男生与女生的人数之比为11:13,男生中有30人表示对冰壶运动有兴趣,女生中有15人表示对冰壶运动没有兴趣.
(1)完成2×2列联表,并回答能否有99%的把握认为“对冰壶是否有兴趣与性别有关”?
有兴趣 | 没有兴趣 | 合计 | |
男 | 30 | ||
女 | 15 | ||
合计 | 120 |
(2)若将频率视为概率,现再从该校全体学生中,采用随机抽样的方法每次抽取1名学生,抽取5次,记被抽取的5名学生中对冰壶有兴趣的人数为X,若每次抽取的结果是相互独立的,求X的分布列,期望和方差.
附:参考公式![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
临界值表:
P(K2≥K0) | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
K0 | 2.072 | 2.076 | 3.841 | 5.024 | 6.635 |