题目内容
3.已知A∪B∪C={a,b,c,d,e},A∩B={a,b,c},c∈A∩B∩C,则符合上述条件的{A,B,C}共有100组.分析 由A∩B={a,b,c},可知集合A,B必含元素a,b,c,且无其它公共元素,又由c∈A∩B∩C推出C的元素的情况,分类讨论满足条件的集合个数,结合A∪B∪C={a,b,c,d,e},最后综合讨论结果,可得答案.
解答 解:∵A∩B={a,b,c},
∴集合A,B必含元素a,b,c,且无其它公共元素,c∈A∩B∩C,C中必有c,不会含有a,b.
(1)当A={a,b,c}时,
B共有4种不同情况,
①B={a,b,c},C必含c,d,e;可能含有a,b;共有4种;
②B={a,b,c,d},C必含c,e;可能含有a,b,d;共有8种;
③B={a,b,c,e},C必含c,d;可能含有a,b,e;共有8种;
④B={a,b,c,d,e},C必含c;可能含有a,b,d,e;共有16种.
符合上述条件的{A,B,C}共有36种.
(2)当A={a,b,c,d}时,
B共有2种不同情况:
①B={a,b,c},C必含c,e;可能含有a,b,d;共有8种;
②B={a,b,c,e},C必含c;可能含有a,b,d,e;共有16种;
符合上述条件的{A,B,C}共有24种不同情况;
(3)同理当A={a,b,c,e}时,由(2)可知共有24种不同情况;
(4)当A={a,b,c,d,e}时,
B={a,b,c},C必含有c,可能含有a,b,d,e;共有16种情况;
综上,共有36+24+24+16=100种不同情况;
故答案为:100.
点评 本题考查的知识点是满足条件的集合个数,考查分类讨论思想的应用,考查计数原理的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.某高中在一次数学考试中随机抽取100名学生的成绩,按成绩分组,得到的频率分布表如图所示
(Ⅰ)求出频率分布表中①、②位置相应的数据;
(Ⅱ)为了能选拔出最优秀的学生参加数学竞赛,学校决定在成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮测试,求第3、4、5组每组各抽取多少名学生进入第二轮测试?
(Ⅲ)在(Ⅱ)的前提下,学校决定在6名学生中随机抽取2名学生进行抽查,求第4组至少有一名学生被抽查的概率?
| 组号 | 分组 | 频数 | 频率 |
| 第1组 | [75,90] | 5 | 0.05 |
| 第2组 | (90,105] | ① | 0.35 |
| 第3组 | (105,120] | 30 | ② |
| 第4组 | (120,135] | 20 | 0.20 |
| 第5组 | (135,150] | 10 | 0.10 |
| 合计 | 100 | 1.00 | |
(Ⅱ)为了能选拔出最优秀的学生参加数学竞赛,学校决定在成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮测试,求第3、4、5组每组各抽取多少名学生进入第二轮测试?
(Ⅲ)在(Ⅱ)的前提下,学校决定在6名学生中随机抽取2名学生进行抽查,求第4组至少有一名学生被抽查的概率?
14.若tan(θ+$\frac{π}{4}$)=-3,则$\frac{sin2θ}{1+cos2θ}$=( )
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
11.直线$\sqrt{3}$x+3y+1=0的倾斜角是( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
18.f(x)=-2x2+mx-3在(-∞,3]上是增函数,则实数m的取值范围是( )
| A. | {1,2} | B. | [6,+∞) | C. | [12,+∞) | D. | (-∞,6] |
8.“0<a<4”是“命题“?x∈R,不等式x2+ax+a≥0成立,为真命题”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
15.执行下面的程序框图,若p=0.95,则输出的n=( )
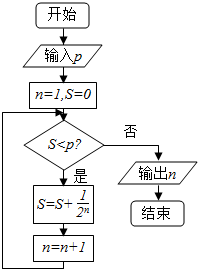

| A. | 4 | B. | 5 | C. | 6 | D. | 7 |