题目内容
【题目】如图,三棱锥D-ABC中,![]()
![]()
![]() ,E,F分别为DB,AB的中点,且
,E,F分别为DB,AB的中点,且![]() .
.
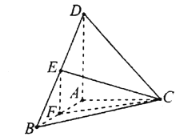
(1)求证:平面![]() 平面ABC;
平面ABC;
(2)求点D到平面CEF的距离.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)取BC的中点G,连接AG,DG,可证![]() 平面DAG,可得
平面DAG,可得![]() ,再由
,再由![]() ,
,![]() ,可证
,可证![]() ,可得
,可得![]() 平面ABC,即可证明结论;
平面ABC,即可证明结论;
(2)由条件可得点D到平面CEF的距离等于点B到平面CEF的距离,求出三棱锥![]() 的体积和
的体积和![]() 的面积,用等体积法,即可求解.
的面积,用等体积法,即可求解.
(1)如图,取BC的中点G,连接AG,DG,
因为![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() ,
,
又因为![]() ,
,
所以![]() 平面DAG,所以
平面DAG,所以![]() .
.
因为E,F分别为DB,AB的中点,所以![]() .
.
因为![]() ,即
,即![]() ,则
,则![]() .
.
又因为![]() ,所以
,所以![]() 平面ABC,
平面ABC,
又因为![]() 平面DAB,所以平面
平面DAB,所以平面![]() 平面ABC.
平面ABC.
(2)因为点E为DB的中点,
所以点D到平面CEF的距离等于点B到平面CEF的距离.
设点D到平面CEF的距离为h,
因为![]() ,又因为
,又因为![]() 平面ABC,
平面ABC,
所以![]() ,
,
在![]() 中,
中,![]()
![]()
![]() .
.
所以![]() ,
,
在![]() 中,
中,![]()
![]()
![]() ,
,
所以 ,
,
又因为![]()
![]()
![]()
![]()
![]() ,
,
所以![]() ,
,
而![]()
![]() ,
,
则![]()
![]()
![]() .
.
所以点D到平面CEF的距离为![]() .
.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案【题目】已知某保险公司的某险种的基本保费为![]() (单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 |
|
保费(元) |
|
|
|
|
|
随机调查了该险种的400名续保人在一年内的出险情况,得到下表:
出险次数 | 0 | 1 | 2 | 3 |
|
频数 | 280 | 80 | 24 | 12 | 4 |
该保险公司这种保险的赔付规定如下:
出险序次 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次及以上 |
赔付金额(元) |
|
|
|
| 0 |
将所抽样本的频率视为概率.
(Ⅰ)求本年度续保人保费的平均值的估计值;
(Ⅱ)按保险合同规定,若续保人在本年度内出险3次,则可获得赔付![]() 元;若续保人在本年度内出险6次,则可获得赔付
元;若续保人在本年度内出险6次,则可获得赔付![]() 元;依此类推,求本年度续保人所获赔付金额的平均值的估计值;
元;依此类推,求本年度续保人所获赔付金额的平均值的估计值;
(Ⅲ)续保人原定约了保险公司的销售人员在上午10:30~11:30之间上门签合同,因为续保人临时有事,外出的时间在上午10:45~11:05之间,请问续保人在离开前见到销售人员的概率是多少?