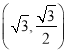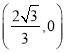题目内容
【题目】有一矩形硬纸板材料(厚度忽略不计),一边![]() 长为6分米,另一边足够长.现从中截取矩形
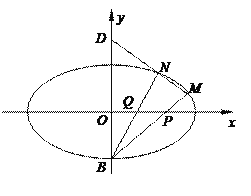
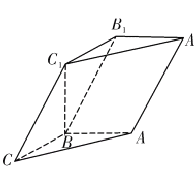
长为6分米,另一边足够长.现从中截取矩形![]() (如图甲所示),再剪去图中阴影部分,用剩下的部分恰好能折卷成一个底面是弓形的柱体包装盒(如图乙所示,重叠部分忽略不计),其中
(如图甲所示),再剪去图中阴影部分,用剩下的部分恰好能折卷成一个底面是弓形的柱体包装盒(如图乙所示,重叠部分忽略不计),其中![]() 是以
是以![]() 为圆心、
为圆心、![]() 的扇形,且弧
的扇形,且弧![]() ,
,![]() 分别与边
分别与边![]() ,
, ![]() 相切于点
相切于点![]() ,
, ![]() .
.
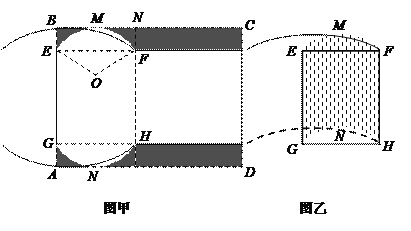
(1)当![]() 长为1分米时,求折卷成的包装盒的容积;
长为1分米时,求折卷成的包装盒的容积;
(2)当![]() 的长是多少分米时,折卷成的包装盒的容积最大?
的长是多少分米时,折卷成的包装盒的容积最大?
【答案】(1)当![]() 长为1分米时,折卷成的包装盒的容积为
长为1分米时,折卷成的包装盒的容积为![]() 立方分米.(2)当
立方分米.(2)当![]() 的长为2分米时,折卷成的包装盒的容积最大
的长为2分米时,折卷成的包装盒的容积最大
【解析】试题分析:(1)先根据扇形面积减去三角形面积得弓形面积,即为柱体底面积,再根据柱体体积公式求体积(2)同(1)先计算底面积,再表示高,代入柱体体积公式得容积函数关系式,最后利用导数求最值
试题解析:解:(1)在图甲中,连接![]() 交
交![]() 于点
于点![]() .设
.设![]() ,
,
在![]() 中,因为
中,因为![]() ,所以
,所以![]() ,则
,则![]() .
.
从而![]() ,即
,即![]() .
.
故所得柱体的底面积![]()
![]() .
.
又所得柱体的高![]() ,
,
所以![]()
![]() .
.
答:当![]() 长为1分米时,折卷成的包装盒的容积为
长为1分米时,折卷成的包装盒的容积为![]() 立方分米.
立方分米.
(2)设![]() ,则
,则![]() ,所以所得柱体的底面积
,所以所得柱体的底面积
![]()
![]() .
.
又所得柱体的高![]() ,
,
所以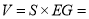
![]() ,其中
,其中![]() .
.
令![]() ,则由
,则由![]() ,
,
解得![]() .
.
列表如下:
|
|
|
|
| + | 0 | - |
| 增 | 极大值 | 减 |
所以当![]() 时,
时, ![]() 取得最大值.
取得最大值.
答:当![]() 的长为2分米时,折卷成的包装盒的容积最大.
的长为2分米时,折卷成的包装盒的容积最大.

练习册系列答案
相关题目