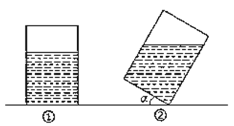
题目内容
【题目】已知数列![]() 中,
中,![]() ,
,![]() ,
,![]() ,且对
,且对![]() 时,有
时,有![]() .
.
(Ⅰ)设数列![]() 满足
满足![]() ,
,![]() ,证明数列
,证明数列![]() 为等比数列,并求数列
为等比数列,并求数列![]() 的通项公式;
的通项公式;
(Ⅱ)记![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
【答案】(Ⅰ)证明见解析;![]() ;(Ⅱ)
;(Ⅱ)![]()
【解析】
(Ⅰ)利用已知等式表示出![]() 和
和![]() ,整理可知
,整理可知![]() ,从而可证得数列
,从而可证得数列![]() 为等比数列,根据等比数列通项公式求得
为等比数列,根据等比数列通项公式求得![]() ;利用配凑的方式可证得数列
;利用配凑的方式可证得数列![]() 为等差数列,利用等差数列通项公式,整理可得
为等差数列,利用等差数列通项公式,整理可得![]() ;(Ⅱ)将
;(Ⅱ)将![]() 代入
代入![]() ,整理可得:
,整理可得:![]() ,利用累乘的方式可求得
,利用累乘的方式可求得![]() ,进而可得
,进而可得![]() ;采用分组求和的方式,分别对
;采用分组求和的方式,分别对![]() 用错位相减的方法求和,对
用错位相减的方法求和,对![]() 采用裂项相消的方法求和,分别求和后加和即可得到结果.
采用裂项相消的方法求和,分别求和后加和即可得到结果.
(Ⅰ)由题意知:![]()
![]()
![]()
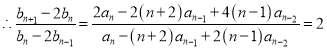
又![]()
![]() 数列
数列![]() 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列
为公比的等比数列
![]()
![]() ,即
,即![]()
![]() 数列
数列![]() 是以
是以![]() 为首项,
为首项,![]() 为公差的等差数列
为公差的等差数列
![]()
![]()
(Ⅱ)由(Ⅰ)知:![]() ,即:
,即:![]()
则:![]() ,
,![]() ,……,
,……,![]()
左右两侧分别相乘可得:![]()
![]()
![]()
![]()
令![]()
![]()
则![]()
![]()
则![]()
![]()

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
【题目】改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:
支付方式 | (0,1000] | (1000,2000] | 大于2000 |
仅使用A | 18人 | 9人 | 3人 |
仅使用B | 10人 | 14人 | 1人 |
(Ⅰ)从全校学生中随机抽取1人,估计该学生上个月A,B两种支付方式都使用的概率;
(Ⅱ)从样本仅使用A和仅使用B的学生中各随机抽取1人,以X表示这2人中上个月支付金额大于1000元的人数,求X的分布列和数学期望;
(Ⅲ)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用A的学生中,随机抽查3人,发现他们本月的支付金额都大于2000元.根据抽查结果,能否认为样本仅使用A的学生中本月支付金额大于2000元的人数有变化?说明理由.