题目内容
7.若函数f(x)(x∈R)是周期为4的奇函数,且在[0,2]上的解析式为$\left\{\begin{array}{l}{x(1-x)\\ \\ 0≤x≤1}\\{sinπx\\ \\ 1<x≤2}\end{array}\right.$,则f($\frac{29}{4}$)+f($\frac{41}{6}$)=$\frac{5}{16}$.分析 通过函数的奇偶性以及函数的周期性,化简所求表达式,通过分段函数求解即可.
解答 解:∵函数f(x)(x∈R)是周期为4的奇函数,
且在[0,2]上的解析式为f(x)=$\left\{\begin{array}{l}{x(1-x)\\ \\ 0≤x≤1}\\{sinπx\\ \\ 1<x≤2}\end{array}\right.$,
则f($\frac{29}{4}$)+f($\frac{41}{6}$)
=f(8-$\frac{3}{4}$)+f(8-$\frac{7}{6}$)
=f(-$\frac{3}{4}$)+f(-$\frac{7}{6}$)
=-f($\frac{3}{4}$)-f($\frac{7}{6}$)
=-$\frac{3}{4}$(1-$\frac{3}{4}$)-sin$\frac{7}{6}$π=-$\frac{3}{16}$+$\frac{1}{2}$=$\frac{5}{16}$.
故答案为:$\frac{5}{16}$
点评 本题考查函数的值的求法,分段函数的应用,考查计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.知a1=1,an+1=$\frac{a_n}{{3{a_n}+1}}$,则数列{an}的通项为an=( )
| A. | $\frac{1}{2n-1}$ | B. | 2n-1 | C. | $\frac{1}{3n-2}$ | D. | 3n-2 |
16.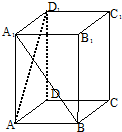 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形,AA1=2AB,则异面直线A1B与AD1所成角的余弦值为( )
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形,AA1=2AB,则异面直线A1B与AD1所成角的余弦值为( )
 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形,AA1=2AB,则异面直线A1B与AD1所成角的余弦值为( )
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形,AA1=2AB,则异面直线A1B与AD1所成角的余弦值为( )| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
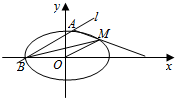 如图,已知离心率为$\frac{\sqrt{3}}{2}$的椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点M(2,1),O为坐标原点,平行于OM的直线l交椭圆C于不同的两点A,B.
如图,已知离心率为$\frac{\sqrt{3}}{2}$的椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点M(2,1),O为坐标原点,平行于OM的直线l交椭圆C于不同的两点A,B.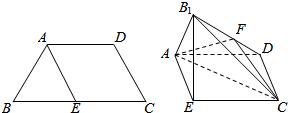 已知四边形ABCD满足AD∥BC,BA=AD=DC=$\frac{1}{2}$BC=a,E是BC的中点,将△BAE沿AE折起到△B1AE的位置,使平面B1AE⊥平面AECD,F为B1D的中点.
已知四边形ABCD满足AD∥BC,BA=AD=DC=$\frac{1}{2}$BC=a,E是BC的中点,将△BAE沿AE折起到△B1AE的位置,使平面B1AE⊥平面AECD,F为B1D的中点.