题目内容
12.极坐标系与直角坐标系xOy有相同的长度单位,以原点o为极点,以x轴正半轴为极轴.曲线C的极坐标方程为 ρ2=4,已知倾斜角为$\frac{π}{4}$的直线?经过点P(1,1).(Ⅰ)写出直线?的参数方程;曲线C的直角坐标方程;
(Ⅱ)设直线?与曲线C相交于A,B两点,求$\frac{1}{|PA|}+\frac{1}{|PB|}$的值.
分析 (Ⅰ)由已知可得直线l的参数方程为$\left\{{\begin{array}{l}{x=1+tcos\frac{π}{4}}\\{y=1+tsin\frac{π}{4}}\end{array}}\right.$,利用ρ2=x2+y2可得曲线C的方程.
(Ⅱ)将$\left\{{\begin{array}{l}{x=1+\frac{{\sqrt{2}}}{2}t}\\{y=1+\frac{{\sqrt{2}}}{2}t}\end{array}}\right.$代入x2+y2=4,化简整理得:${t^2}+2\sqrt{2}t-2=0$.可得|PA|×|PB|=|t1|×|t2|,由于直线l经过圆心,可得|PA|+|PB|=|AB|=4,代入即可得出.
解答 解:(Ⅰ)直线l的参数方程为$\left\{{\begin{array}{l}{x=1+tcos\frac{π}{4}}\\{y=1+tsin\frac{π}{4}}\end{array}}\right.$,即$\left\{{\begin{array}{l}{x=1+\frac{{\sqrt{2}}}{2}t}\\{y=1+\frac{{\sqrt{2}}}{2}t}\end{array}}\right.$,
曲线C的方程x2+y2=4.
(Ⅱ)将$\left\{{\begin{array}{l}{x=1+\frac{{\sqrt{2}}}{2}t}\\{y=1+\frac{{\sqrt{2}}}{2}t}\end{array}}\right.$代入x2+y2=4,化简整理得:${t^2}+2\sqrt{2}t-2=0$.
∴|PA|×|PB|=|t1|×|t2|=|t1×t2|=|-2|=2,
∵直线l经过圆心,∴|PA|+|PB|=|AB|=4,
∴$\frac{1}{{|{PA}|}}+\frac{1}{{|{PB}|}}$=$\frac{{|{PA}|+|{PB}|}}{{|{PA}|×|{PB}|}}=\frac{4}{2}=2$.
点评 本题考查了直线参数方程的应用、直角坐标方程与极坐标方程互化,考查了推理能力与计算能力,属于中档题.

| A. | $\frac{x}{2}$-3<$\frac{x}{3}$-3 | B. | $\left\{\begin{array}{l}{x-2<0}\\{2-3x>1}\end{array}\right.$ | C. | x2-2x>0 | D. | |x-1|<2 |
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
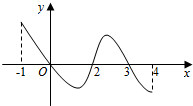 已知函数f(x)的定义域为[-1,4],部分对应值如表,
已知函数f(x)的定义域为[-1,4],部分对应值如表,| x | -1 | 0 | 2 | 3 | 4 |
| f(x) | 1 | 2 | 0 | 2 | 0 |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |