题目内容
18．已知正实数a、b满足a2+b+3=ab，则a+b的最小值为3+4$\sqrt{2}$．分析 将a2+b+3=ab化为（2a-2）（b-a-1）=8，再利用基本不等式，求解不等式即可求得a+b的取值范围，从而得到a+b的最小值．
解答 解：由a2+b+3=ab得a2-2a+1-b（a-1）+2（a-1）=-4，
即（a-1）2-b（a-1）+2（a-1）=-4，
∴（a-1）（a-1-b+2）=-4
∴（2a-2）（b-a-1）=8，
∴8=（2a-2）（b-a-1）≤$（\frac{2a-2+b-a+1}{2}）^{2}$=$（\frac{a+b-3}{2}）^{2}$
解得a+b≥3+4$\sqrt{2}$，取等号的条件是2a-2=b-a-1且（2a-2）（b-a-1）=8，解得a=$\sqrt{2}$-1，b=3$\sqrt{2}$，
∴a+b的最小值为3+4$\sqrt{2}$．
故答案为：3+4$\sqrt{2}$．
点评 本题考查了基本不等式在最值问题中的应用．在应用基本不等式求最值时要注意“一正、二定、三相等”的判断．运用基本不等式解题的关键是寻找和为定值或者是积为定值，难点在于如何合理正确的构造出定值．属于中档题
练习册系列答案
相关题目
9．设函数f（x）=2x3+3ax2+3bx+8c在x=1及x=2时取得极值，若对于任意的x∈[0，3]，都有f（x）＜c2成立，则实数c的取值范围为（ ）
| A． | （-1，9） | B． | （-9，1） | C． | （-∞，-1）∪（9，+∞） | D． | （-∞，-9）∪（1，+∞） |
13．
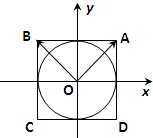如图，在平面直角坐标系xoy中，圆x2+y2=r2（r＞0）内切于正方形ABCD，任取圆上一点P，若$\overrightarrow{OP}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$（m，n∈R），则$\frac{1}{4}$是m2，n2的等差中项，现有一椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）内切于矩形ABCD，任取椭圆上一点P，若$\overrightarrow{OP}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$（m，n∈R），则m2，n2的等差中项为（ ）
如图，在平面直角坐标系xoy中，圆x2+y2=r2（r＞0）内切于正方形ABCD，任取圆上一点P，若$\overrightarrow{OP}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$（m，n∈R），则$\frac{1}{4}$是m2，n2的等差中项，现有一椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）内切于矩形ABCD，任取椭圆上一点P，若$\overrightarrow{OP}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$（m，n∈R），则m2，n2的等差中项为（ ）| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | 1 |
3．下列不等式（组）的解为{x|x＜0}的是（ ）
| A． | $\frac{x}{2}$-3＜$\frac{x}{3}$-3 | B． | $\left\{\begin{array}{l}{x-2＜0}\\{2-3x＞1}\end{array}\right.$ | C． | x2-2x＞0 | D． | |x-1|＜2 |
4．
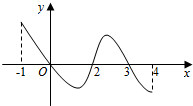已知函数f（x）的定义域为[-1，4]，部分对应值如表，
f（x）的导函数y=f′（x）的图象如图所示．当1＜a＜2时，函数y=f（x）-a的零点的个数为（ ）
已知函数f（x）的定义域为[-1，4]，部分对应值如表，| x | -1 | 0 | 2 | 3 | 4 |
| f（x） | 1 | 2 | 0 | 2 | 0 |
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |