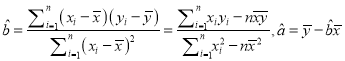题目内容
【题目】给出下列![]() 个结论:
个结论:
①棱长均相等的棱锥一定不是六棱锥;
②函数![]() 既不是奇函数又不是偶函数;
既不是奇函数又不是偶函数;
③若函数![]() 的值域为
的值域为![]() ,则实数
,则实数![]() 的取值范围是
的取值范围是![]() ;
;
④若函数![]() 满足条件
满足条件![]() ,则
,则![]() 的最小值为
的最小值为![]() .
.
其中正确的结论的序号是:______. (写出所有正确结论的序号)
【答案】①,③,④
【解析】
对所给的四个结论分别进行分析、判断后可得正确的结论的序号.
对于①,由平面几何知识可得,正六边形的中心到各顶点的距离等于边长,此时中心与各顶点构成平面图形,所以棱长均相等的棱锥一定不是六棱锥.所以①正确.
对于②,由![]() 得
得![]() ,故函数的定义域为
,故函数的定义域为![]() ,所以
,所以![]() ,所以
,所以![]() ,为偶函数.所以②不正确.
,为偶函数.所以②不正确.
对于③,设![]() ,由于函数的值域为
,由于函数的值域为![]() ,所以
,所以![]() 能够取尽所有的正数,即函数
能够取尽所有的正数,即函数![]() 的图象与x轴有公共点.当
的图象与x轴有公共点.当![]() 时,
时,![]() ,满足题意;当
,满足题意;当![]() 时,则有
时,则有![]() ,解得
,解得![]() .综上可得实数
.综上可得实数![]() 的取值范围是
的取值范围是![]() ,所以③正确.
,所以③正确.
对于④,以![]() 代替
代替![]() 中的
中的![]() 可得
可得![]() ,由
,由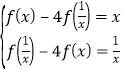 消去
消去![]() 整理得
整理得![]() ,所以
,所以![]() ,当且仅当
,当且仅当![]() ,即
,即![]() 时等号成立.所以④正确.
时等号成立.所以④正确.
综上可得正确结论的序号为①③④.
故答案为①③④.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目